近年量子コンピュータが注目されているが、応用先については「創薬」「金融」といった抽象的なものはよく取り上げられるが実際どの程度の具体的な事例に適用できるかについてはあまり耳にしないと思う。
今回はIBMとモデルナ(新型コロナウイルスのmRNAワクチンで有名になった会社)が実際に協働して量子コンピュータを使ったmRNA(メッセンジャーRNA)の二次構造の予測についての研究を紹介する。(私の勉強のために)手法にそれなりの割合を割いているが、結果だけ知りたい人は最後の方に飛ばすと良い。
mRNA secondary structure prediction using utility-scale quantum computers
Alevras, D., Metkar, M., Yamamoto, T., Kumar, V., Friedhoff, T., Park, J. E., … & Galda, A. (2024). mRNA secondary structure prediction using utility-scale quantum computers. arXiv preprint arXiv:2405.20328.
本文中の図などは CC-BY 4.0 にて引用している。
mRNAの二次構造とその予測について
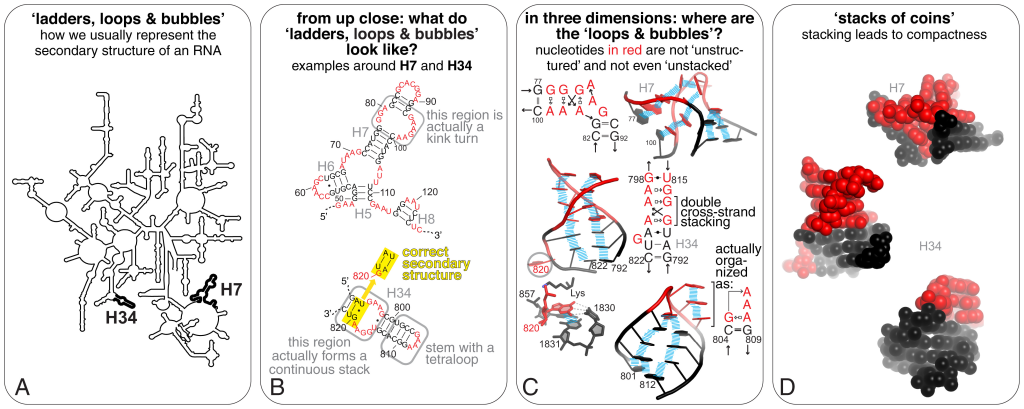
RNAは(学部生向けの)教科書的には一本鎖でそのままDNAから転写されて翻訳される、みたいなイメージがついていると思うが、実際は複雑な構造を取ることがある。
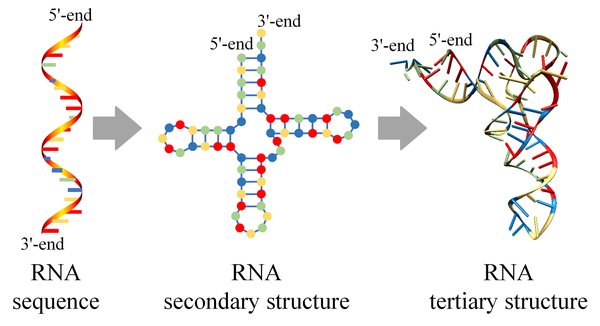
Zhao et al (2021)より引用 CC-BY 4.0
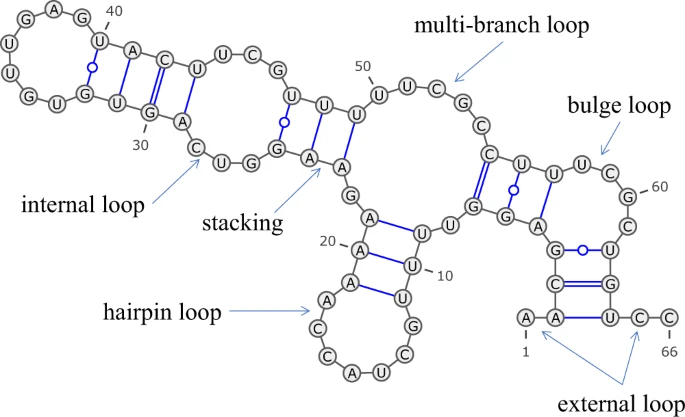
二次構造としては、内部ループ、スタッキング、多分岐ループ (multi-branch loop)、バルジループ (Bulge loop)、そしてよく知られたヘアピンループ (Hairpin loop) などが知られている。
こうしたものを予測する古典的なアプローチとしては Zuker のアルゴリズムがよく知られている(Zuker, 1989a)。このアルゴリズムは動的計画法を採用しており、最小自由エネルギーを求めることで二次構造を予測する(Zuker, 1989b)。
そうした計算法から現在は機械学習を用いた予測が徐々に流行りだしてきている(Zakov et al., 2011; Sato et al., 2021など)。
ただ一方、こうしたRNAの二次構造の機械学習による予測はRNAファミリー内(相同なRNAのセット)では機能するものの、ファミリーを超えてまではまだ一般化されたモデルというものは(この論文が書かれた時点では)ないとされている(Szikszai et al., 2022)。
従来の(機械学習ではない)アルゴリズムはNP完全問題であることが知られている(Lyngsø and Pedersen, 2000)。そこで量子コンピュータを使って効率的にこの問題を解くことができないか、というものである。量子コンピュータを使えばNP完全問題について計算量が削減される例は多く知られている。
少し余談にはなるが、上記のような「二次構造」だけでなく、三次構造についても研究が進んでいる。ワトソン・クリック型塩基対だけでなく、もっとねじ曲がったりスタッキング相互作用などにより複雑な形を取ることが知られている(Vicens & Kieft, 2022)。
量子コンピュータを使った二次構造予測の先行研究
量子コンピュータ、とりわけ量子アニーリング型を用いたmRNAの二次構造の予測というものがいくつか行われている。このブログでも何度か触れているが、アニーリング型の量子コンピュータを開発しているD-waveの量子コンピュータを使った研究では、旧来の手法と同等の精度を出すことが可能であることを示唆している(Fox et al., 2022)。が、配列が長くなるほど予測は困難になる。
ただアニーリング型の問題点としては、汎用性が低いためにアルゴリズムに制限があるというものがある。
より汎用性が高いゲート型の量子コンピュータのアルゴリズムの例としては、Quantum Approximate Optimazation Algorithm (量子近似最適化アルゴリズム; QAOA) を使った研究(ただしpyQPandaという量子計算シミュレータを使っている)などがある (Jiang et al., 2023)。
ただ、現在のゲート型のノイズがある量子コンピュータ(NISQ)では最小固有値を見つけるには時間がかかるため(ノイズが入って)実現困難なものがある。そこで短い量子回路を利用するVariational Quantum Eigensolver (変分量子固有値ソルバー法; VQE) が提案されている。QAOAやVQEは最適化問題の基底状態と十分に重なり合う量子状態を見つけることが目的である。これまでは量子コンピュータのハードの問題(量子ビットが少ないなど)があったために少数の量子ビットやシミュレーション上での計算が多かった。最近では100量子ビットを超えた量子コンピュータがIBMで開発される (Kim et al., 2023) など、要は「研究で実際に使える段階」に入りつつあるのではないかと考えている。
前置きが長くなったが、今回紹介する論文 (Alevras et al., 2024) ではこうした背景を踏まえて、「比較的長いmRNA」を汎用的なゲート型量子コンピュータで解く実現可能性を調査したものである。本研究では変分量子アルゴリズムがIBMの量子コンピュータ上できちんと実行できるかどうかの検証的な面が大きい。
研究の手法と概要
この研究では従来のVQEアルゴリズムを改良した、Conditional Value at Risk Variational Quantum Eigensolver (条件付きリスク値変分量子固有値ソルバー; CVaR-VQE)を使用し、エネルギー固有関数のCVaR値 (Barkoutsos et al., 2020) を目的関数とすることでより良い収束を実現している。ちなみにこのCVaR値の論文の著者もIBM所属。古典シミュレーションと量子ハードウエアの両方を使う最適化問題において優れた収束が速くなることが示されている。これに加えて、中西・藤井・藤堂 (NFT) 最適化手法 (Nakanishi et al., 2020) を用いている。
ハードウェアのノイズに対しては two-local ansatz を使用することで比較的高い堅牢性を実現している (Oliv et al., 2022)。Qiskitで利用可能。
まず、二次構造の予測問題をバイナリ最適化問題 (Binary Optimization)として定式化する。その式をIBMのCPLEXという最適化ソフトウェアを用いて解を求めているが、CPLEXなどの従来の方式では実行時のスケーリング(より長いmRNAを解く場合)がうまくいかない、ということを示している。次に量子ハードウエアと古典シミュレーションの両方を使って、15-42塩基のRNA配列長の二次構造に対し、10-80量子ビットの範囲の最適化問題で計算している。これまでの研究では42塩基長まで長い配列の量子コンピュータでの二次構造は予測できていなかったため、初めての例となる。
こうしたRNAの二次構造を予測する研究というものは、RNAベースの創薬・治療法を設計するうえで重要視されるようになってきている。
定式化
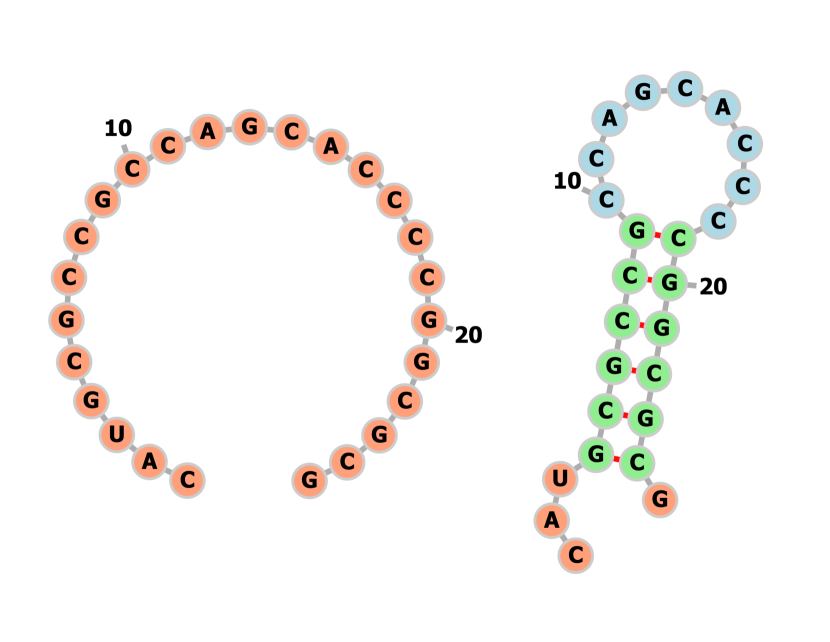
RNAは4種の塩基から成る。AUGC。これのポリマーがRNA鎖である。生体内において、RNAは疎水性や塩基対形成、スタッキング相互作用などによりコンパクトな構造を取ることがよく知られている(Vicens & Kieft, 2022)。プライマーなどを発注するときにヘアピン構造を取らないように気をつけろ、とかいう話を耳にする実験系研究者は多いだろう。
今回の研究では一番単純なワトソン・クリック型塩基対(A-U, C-Gペア)に基づいた二次構造を予測する。ただし、どの塩基同士で塩基対を生成するかは最適化問題を問いてみないことにはわからない。実際問題、この最適な折りたたみの特徴は完全には解明されていないために近似的に求めることとなる。場合によっては複数の最適な構造が存在する可能性がある。
この最適化問題は、熱力学的な問題である。上の図の例でいうと、直鎖で存在している場合(図左)のループを自由エネルギーが最小になるように(熱力学第二法則)ワトソン・クリック型塩基対を作る方向に反応が進む(図右)。これは直鎖で存在している状態よりもスタッキングやペアリングを形成する状態のほうが自由エネルギーが小さくなる場合に起こり得る。長い塩基(ステム)は通常二次構造を取ることで安定となるが、一本鎖領域は不安定さをもたらす傾向がある。ここで計算したいものは、生理学的条件下において、RNAが最も採用する可能性の高いコンフォメーション(折りたたみの状態)、つまり最小自由エネルギー (MFE) を取る構造である。
これまでのアプローチ
これまでのアプローチとしてどのようにMFEを求めるかについて触れておく。RNAの二次構造を予測する多くのアプローチはMFEの最小化を通じて構造を特定する物が多い。ただこれは最適化問題としてみると一般にNP困難であるとされる。NP困難とは簡単に言うと計算量が例えば指数関数的に増えるなどして解く自体は可能ではあるが計算量的に現実には非常に困難であるような問題のことである。
そうした問題に対しては近似的に求めることで解を求めようとする。動的計画法、遺伝的アルゴリズム、機械学習など。RNAの二次構造予測の問題は二次制約なしバイナリ最適化 (Quadratic Unconstrained Binary Optimization; QUBO) 問題として定式化できる。これまでの量子コンピュータ(アニーリング型)を使った手法ではバイナリ変数を最小化する目的関数の開発に焦点を当てた研究があった(Fox et al., 2022; Zaborniak et al., 2022)。(本研究で用いる量子コンピュータはゲート型の量子コンピュータである。この研究では、数学的プログラミングを使用して問題をバイナリ変数で表現し、その結果得られたプログラムをQUBOに変換し、汎用量子コンピュータで解くことを目的としている)
動的計画法
最適な折りたたみを近似する方法のひとつは、対になる塩基の数を最大化することである。これまでに動的計画法に基づいた Nussinov algorithm (ヌシノフのアルゴリズム) が開発されている (Nussinov and Jacobson, 1980)。Wikipediaにどんなものかまとまっている。高速であるのと、精度としては65-73%程度の性能である(Mathews et al., 1999)。
数理計画法
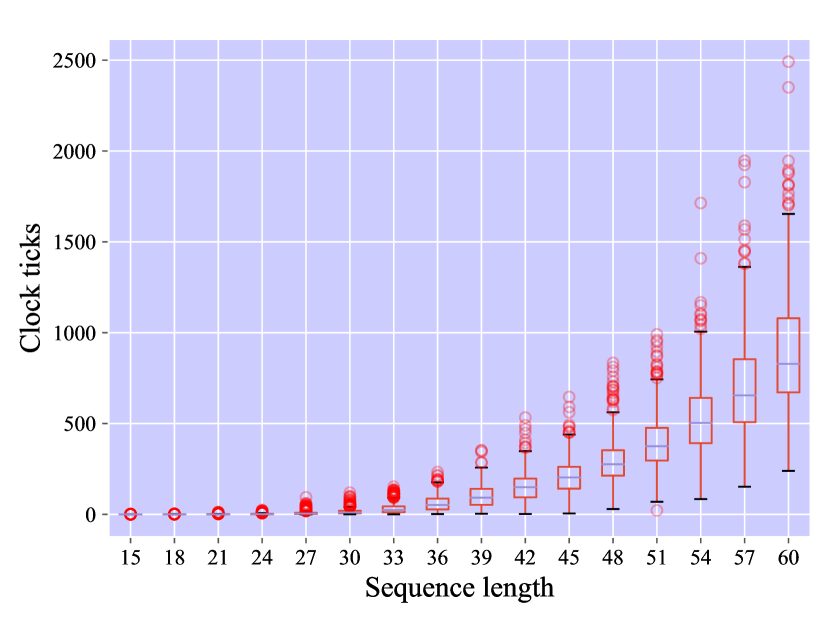
古典的なアプローチとしてよく使われるものとしては他に数理計画法がある。このモデルでは変数と制約の数が非常に多くなるが、現在使われているソルバーでは妥当な規模の問題を処理するには十分なほどに洗練されている(らしい)。これは二次バイナリ最適化問題に落とし込まれる。後述する量子コンピュータを使った方法と比較するため、IBMのCPLEX (数理計画法のソルバー) を使って15-60ヌクレオチドのシーケンスを生成し、二次バイナリ問題を計算した。実行時間とシーケンスの長さの関係は下の図の通り。指数関数的に増加しているのがわかる。プログラム内の時間単位を縦軸に取っているが、実際は数秒程度で求まるようだ。
量子的なアプローチ
QUBO (Quadratic Unconstrained Binary Optimization) の定式化
先述の数理計画法の定式化は二次制約付きバイナリ問題最適化問題(QCBO)である。これをQUBO問題に変換することで、対応するハミルトニアンを得ることができる。これについてはQiskitですでにライブラリが実装されている。結果として得られるQUBOの目的関数は以下の通り。
\[
\begin{array}{rl}
\text{min} & \displaystyle\sum_{q_i \in Q} e_{q_i} q_i \
& + r \displaystyle\sum_{q_i \in Q} \sum_{q_j \in Q S(q_i)} q_i q_j \
& + p \displaystyle\sum_{q_i \in Q} \sum_{q_j \in Q UA} q_i (1 – q_j) \
& + t \displaystyle\sum_{q_i, q_j \in Q C} q_i q_j \
\end{array}
\]
\[
\begin{array}
\text{s.t.} & q_i \in \lbrace0, 1\rbrace \quad \forall q_i \in Q
\end{array}
\]
本当は本文中式(1-2)から導き出されるのだが、超簡潔に内容をまとめるとまず塩基\(i\)と\(j\)のペアを\((i, j)\)と表す。ここで、ペアのスタック、\((i, j), (i + 1, j-1), …, (i+k, j-k)\)を\((i,j,k)\)と表す。さらにQuartet(カルテット)として知られる連続する2組のスタックを\((i,j,i+1,j-1\)のように表す。数式だけだとイマイチ想像しにくいだろうから図を下に補足しておく。以下のようなRNA直鎖が存在したとき、単純にワトソン・クリック型塩基対について考えてみる。\(i, j\)などの関係はこういうように表される。
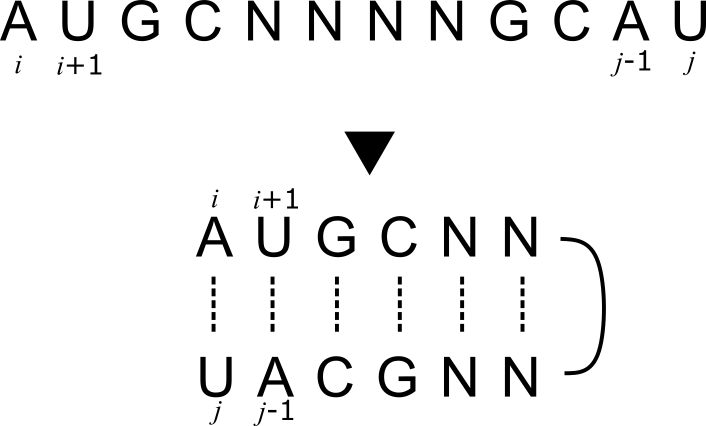
\(q_i\)は各カルテット変数で\(i\)番目のカルテットが選択される場合は1、そうでない場合を0とする。\(e_{q_i}\)はカルテット\(q_i\)に関連する自由エネルギーを表す。また、\(Q\)は有効なカルテットの集合を表す。などなど、個々の変数については本文を参照して欲しい。ここでは上の式によって、RNA二次構造予測問題を解くために上のような目的関数と制約条件を定義した。
CVaRベースのVQE
本研究では CVaR (Conditional Value at Risk) ベースのVQE (変分量子固有値ソルバー)用いて、上記で定義したQUBO問題を解く。VQEは量子化学計算などにおいて、基底エネルギーの値を求めるために用いられる最適化アルゴリズムである(Robert et al., 2021)。VQEは古典コンピュータと量子コンピュータを組み合わせた両方の利点を利用した(主にハミルトニアンの基底状態エネルギーを)効率的に解くソルバーである。
回転角度\(\theta\)によって特徴づけられるユニタリ操作\((U(\theta))\)を使用して、パラメータ化された量子状態\((|\psi(\theta)\rangle = U(\theta)|0\rangle)\)の測定後にサンプリングされたビット列とそれに対応するエネルギーの確率分布を考える。状態\((|\psi(\theta)\rangle\)が目的関数である。この目的関数を最小化する最適なパラメータ\(\theta)\)を見つけることが目標である。これは通常、古典的な最適化手法を使う。
CVaRベースの目的関数は、下位\(\alpha\)分位の平均を用いたものを使用している。エネルギーのサンプリング結果を精進にソートした集合\(\lbrace E_i \rbrace (i \in [1…K])\)を使用し、CVaR(\(\alpha)\)を以下のように定義している。
\[
\text{CVaR}(\alpha) = \frac{1}{\lceil \alpha K \rceil} \sum_{i=1}^{\lceil \alpha K \rceil} E_i
\]
ここで、\(\alpha\)はリスクの水準を表し、典型的には \((0 < \alpha \leq 1)\) の範囲で設定される。\((E_i)\) はサンプルされたビット列のエネルギーで、昇順にソートされている。\(\lceil \alpha K \rceil\) は \((\alpha K)\) の切り上げを表す。
古典的なオプティマイザ
最近のいくつかの研究で、変分法に対する古典的な最適化モデルの性能をNISQにおける堅牢性について検討している(Lavrijsen et al., 2020; Pellow-Jarman et al., 2023)。やはり現在の量子コンピュータではノイズがどうしても問題になるために、それをいかに織り込み済みのものとしてオプティマイザを作るかが重要となっている。中でもNFTアルゴリズム(中西・藤井・藤堂 最適化手法) (Nakanishi et al., 2020) はノイズの影響下においても比較的優れていることがわかっている古典的なオプティマイザである。
本研究においては期待値の代わりとしてCVaR値を使用している。\(\alpha < 1\)のとき、CVaRを期待値の代わりとしてNTFが通常よりも早くに収束することが確認されている (\(\alpha = 1\)のときと比較して)。NTFアルゴリズムを使うことで従来の期待値ベースの手法よりも効率的に最適化が行えるということである。
Ansatz
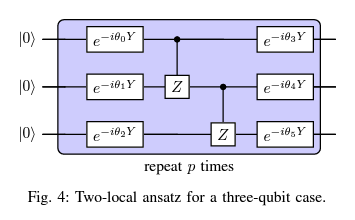
Ansatz (アンザッツ)は物理や数学において使われる用語で、特定の問題を解決するために仮定された関数や形式を指す。量子コンピュータにおいては量子回路の設計の文脈において使用される。
上の図に説明されるように、3量子ビットに対する Two-local Ansatz を使用している。このアンザッツは単一量子ビットのパウリY回転 \(e^{-i\theta Y}\) と2量子ビットの制御Zゲートを組み合わせたものである。このアンザッツはNTFアルゴリズムと互換性があるとしている。
詳細は割愛するが、シミュレーションでは2量子ビットゲートはペアワイズ方式というものを採用している。量子コンピュータのハードウエア上では後述するようにハードウェアの特性評価後に得られた実際のハードウェアサブグラフに量子ビット間で Ansatz が適用される(実在の、物理的な、ハードの話をしている)。
結果
シミュレーション
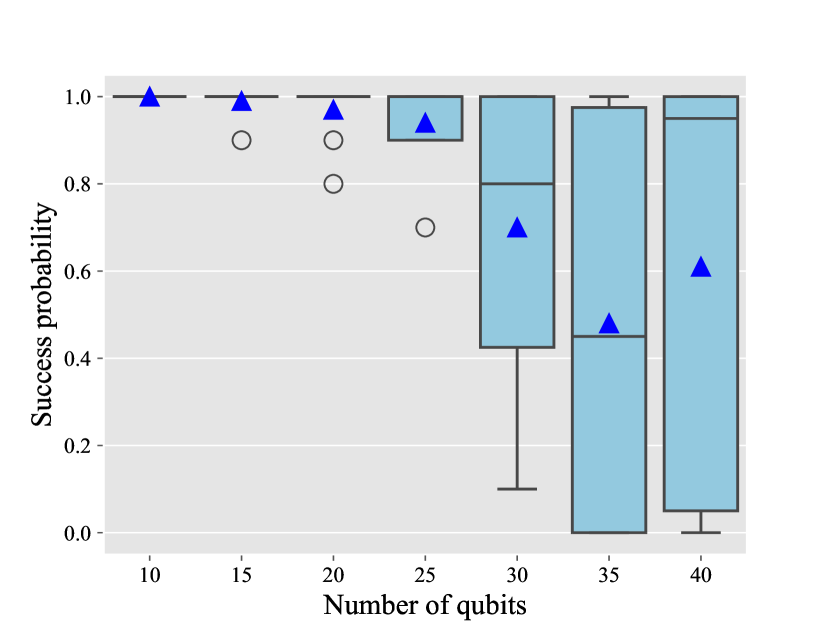
まず CVaR-VQEのノイズフリーシミュレーションを行列積状態 (Matrix Product State; MPS) を使って行った。これはQiskitで提供されているものでできる。ただし、MPSベースのシミュレータの計算コストはエンタングルメントによって指数関数的に増大することが知られている(Vidal, 2003)。NTFアルゴリズムのような古典的な最適化は局所的な最小値に陥りやすいため、問題インスタンスに対してNtrial = 10回の独立したCVaR-VQEの試行を実行した。各 Qbit size について10種類のmRNA配列を調べている。
下の図は10-40量子ビットまでの様々な Problem Instance における成功率を示している。ここでは成功率とは、CPLEXによって得られた解と同じ、最も低いエネルギーを持つビット列(bitstring)が最終的な量子状態である \(|\psi(\theta_f)\rangle\) を測定したあとに見つかった場合を成功し、その割合を成功率と定義している。Qbits が増えるに従って成功率が低くなっていることがわかる。
次にCVaR-VQEアルゴリズムの性能を評価するためのメトリクス、最適性ギャップ(optimality gap; \(\chi\)) について定義し(本文参照)、成功率に加えて解の質を評価している。それが下図である。
見方については、\(\chi\)がゼロより大きい場合、最適解からの偏差が存在することを示している。逆に言えば、\(\chi\)の値が小さいほどCVaR-VQEによって得られた解の質が高いことを示している。
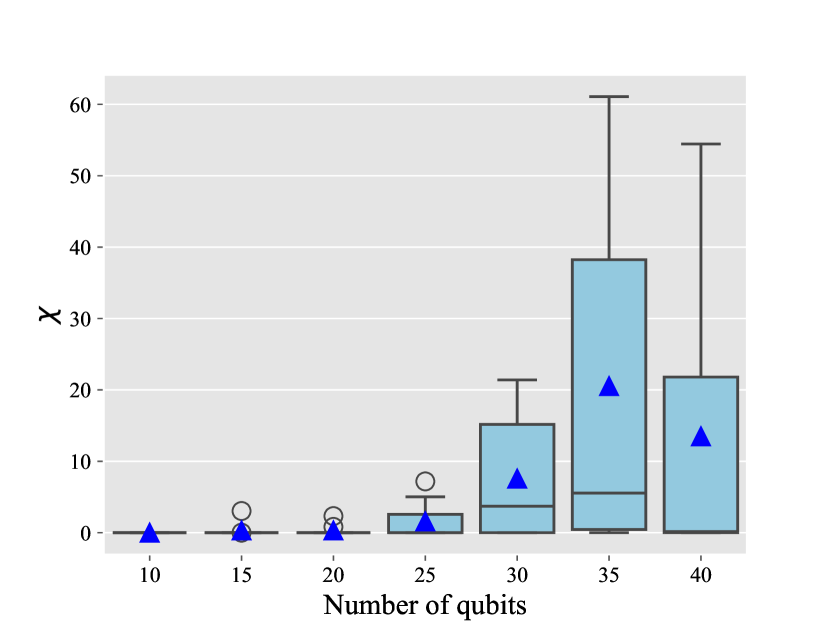
ただ、見てわかるように、量子ビットのサイズが大きくなるにつれてアルゴリズムの性能が低下している。シミュレータ上では計算の都合上回路の階層を浅く設計しているのでそれによる性能の低下だと推測している。アンザッツの層数を増やす必要や、アルゴリズムの改善が必要であると述べている。
量子コンピュータ実機での実行
そして次に量子コンピュータ実機での実行を行った。我々が普段使用している古典コンピュータもArmだのx64だの色々あるように、量子コンピュータも一概にゲート型といっても各会社ごとに仕様が異なる。まずIBM Eagle, Heron プロセッサ(Heronプロセッサは2023年に出たばかりの133量子ビットのプロセッサ)で実行されている。
以前のQiskitの記事にも書いたように、チップの物理的な特性のばらつきがあるために最適化の工程が必要である。
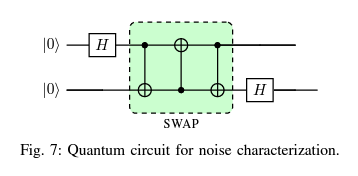
量子ビットの選択
量子コンピュータの物理的なチップ全体でノイズ特性にばらつきがあるため、計算するときの量子ビットをエラー率の小さいハードウェアのサブグラフにマッピングすることが重要になる。
このために、層別フィデリティベンチマーク方式 (McKay et al., 2023) に類似した方法で回路層全体のフィデリティ(忠実度)のベンチマークを行った。単純な2量子ビット回路(Fig.7、上の図)を各レイヤの結合にまたがって個別に実装した。
下図の青、赤、緑で示された三層の結合が量子デバイス上のすべての隣接相互作用をカバーしている。縦軸はフィデリティ、横軸はFig. 8bにおける隣接した量子ビット同士のペアを表している。例えば赤色で一番フィデリティが高い[6,5]は量子デバイス上の配置(Fig. 8b)でも赤色で対応している。
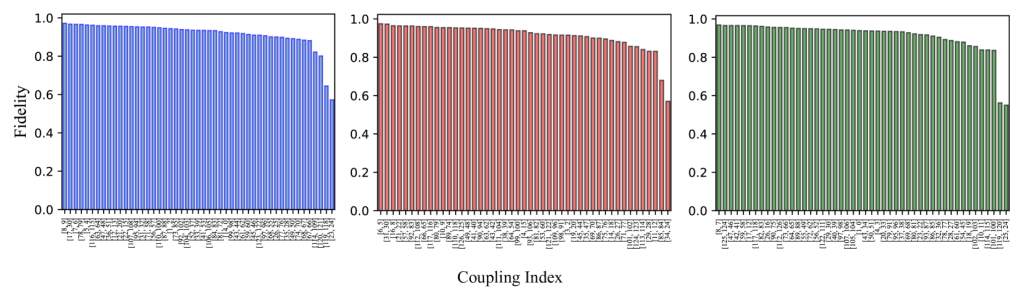
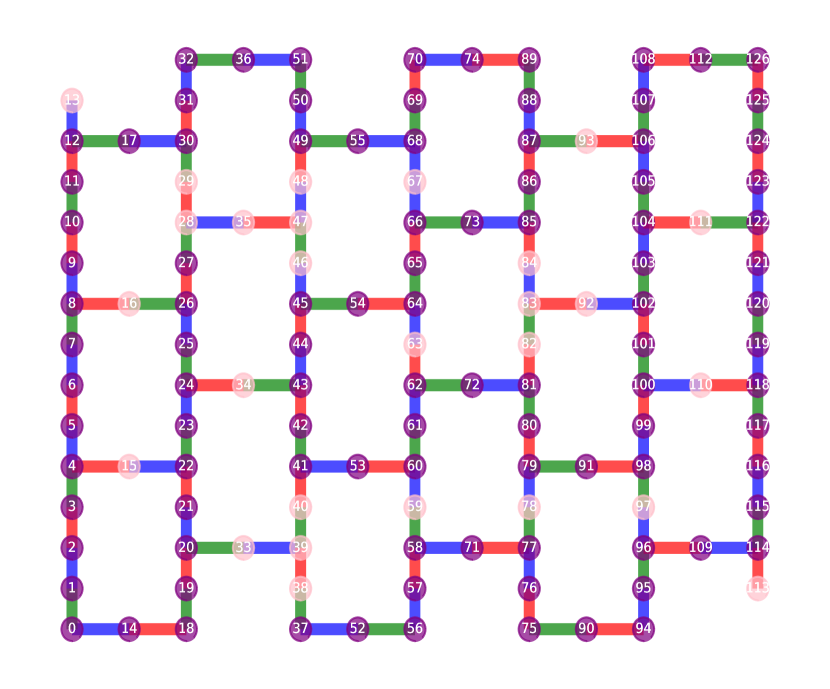
次に、「良い」量子ビットのセットを選ぶために、100個の量子ビットからなる一次元の鎖(chain)を考える。鎖全体で、設定した閾値に満たないフィデリティに満たない量子ビットを計算から除外している。本研究においては0.85を閾値としている。今回はHeronプロセッサ(133量子ビット)を使っているが、こうした除外をしたうえで使用した最大の量子ビットは80だった。
また、この他にもエラー抑制、エラーの緩和を行っている。前にQiskitにおいてトランスパイルしたときはoptimization_level=1(デフォルト)を使用していたが、今回は optimization_level=3 で行っている。
量子コンピュータでmRNAの二次構造を予測した結果
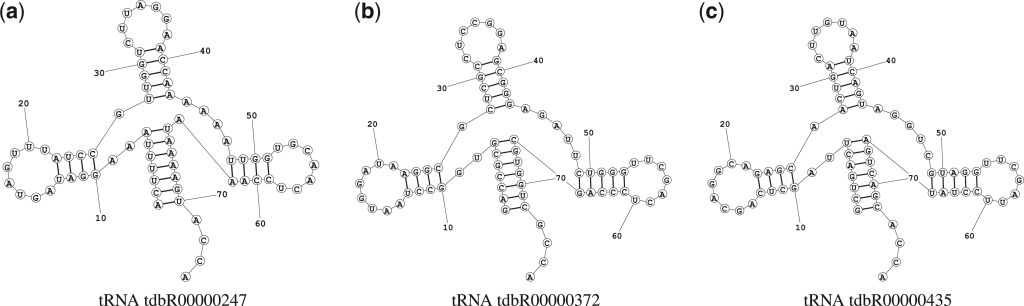
ここからが本編。前置きが長かったと諦めかけた読者もどうかここでコーヒーでも淹れて持ち直して欲しい。本研究ではハードウェア上で3つのmRNA配列の構造予測を行った。(a) 25塩基のmRNA配列に対し26量子ビット、 (b) 30塩基のmRNA配列に対し、40量子ビット、 (c) 30塩基のmRNA配列に対し50量子ビット、の3つ。
これらのインスタンスに対し、それぞれ8回、8回、5回の独立したCVaR-QVEの試行を行った。
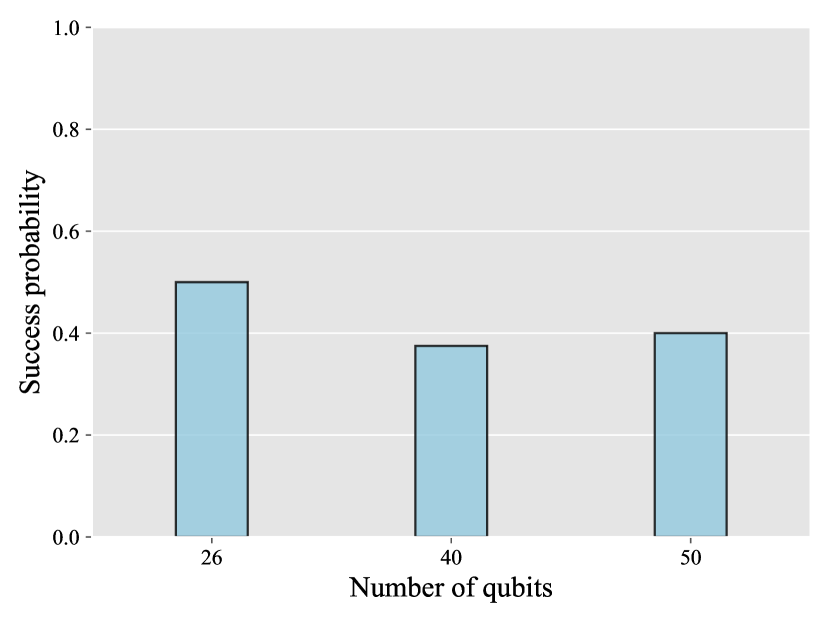
その結果、成功率としてはFig. 10に示されるように概ね0.38以上の確率で成功している(成功とは特定の閾値以下のエネルギーを見つけることに成功したこと、つまり閾値以下の目的関数の値に達したこと)。
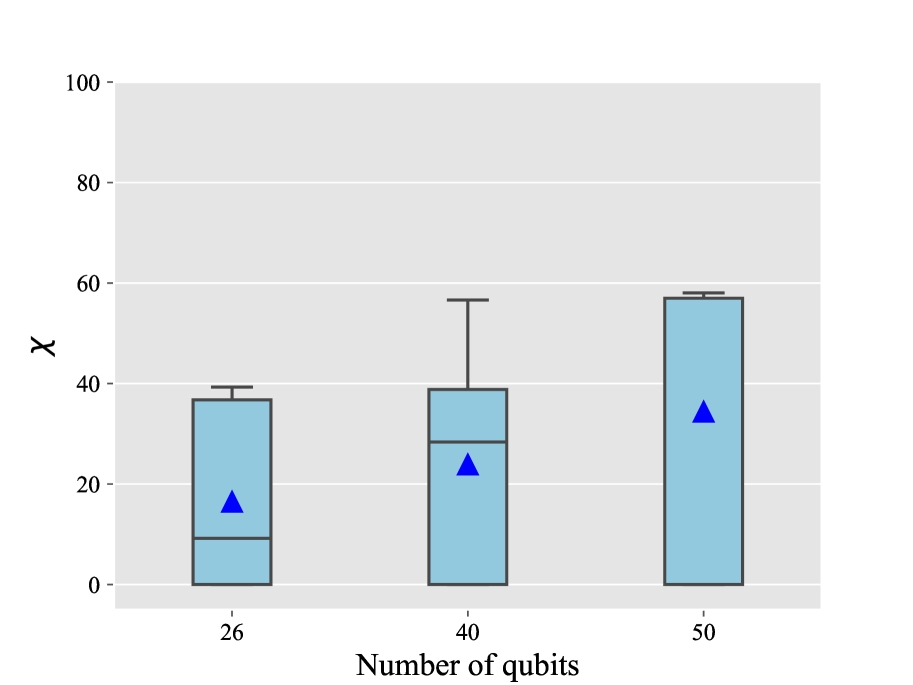
量子コンピュータ上でのCVaR-VQEのギャップ\(\chi\)は34%未満であった。成功率、\(\chi\)、両者ともに量子シミュレータの結果と比べるとずいぶんと劣るが、実機のノイズやチップのばらつきなどの影響が大きく出ているところに起因していると思われる。これは将来的にフォールトトレラントな量子チップの改良に伴って改善されてくだろう。
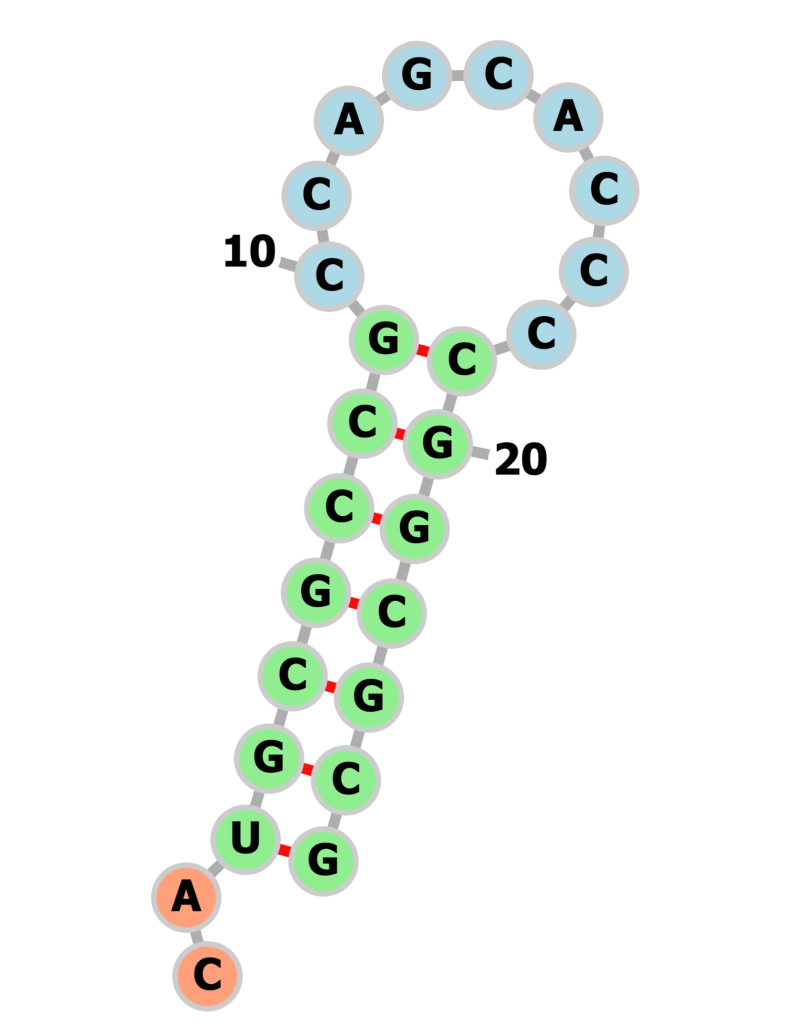
そしてこのように実際に最適化された二次構造を予測してくれたものがこちら。
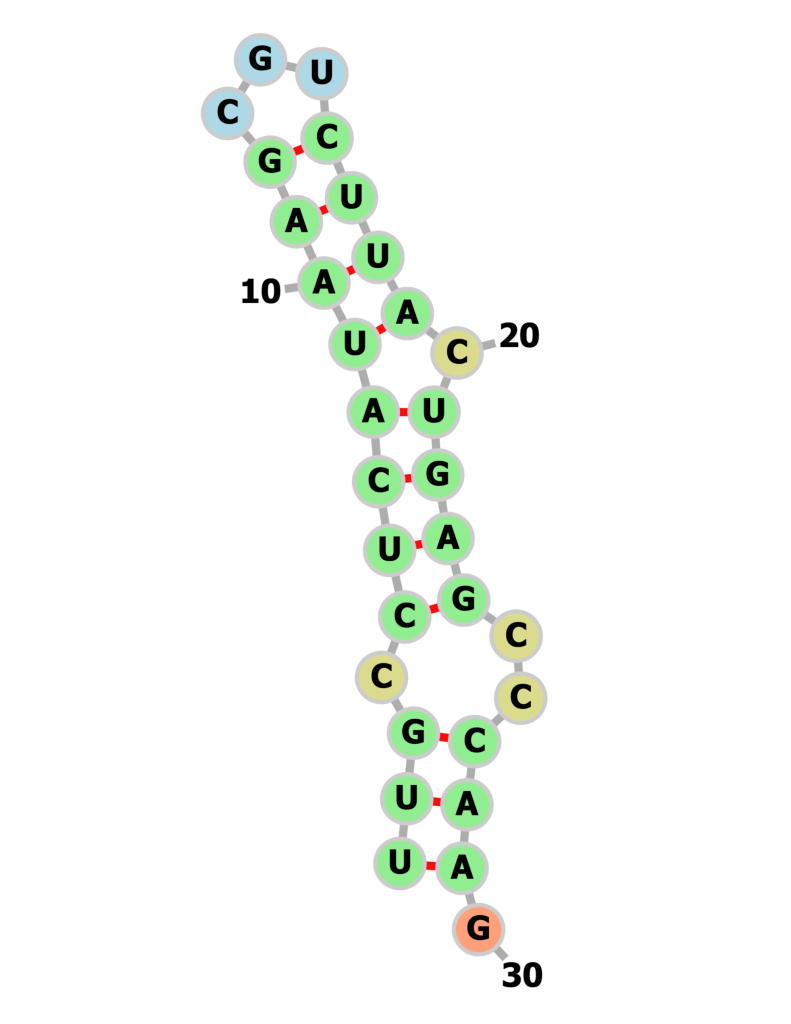
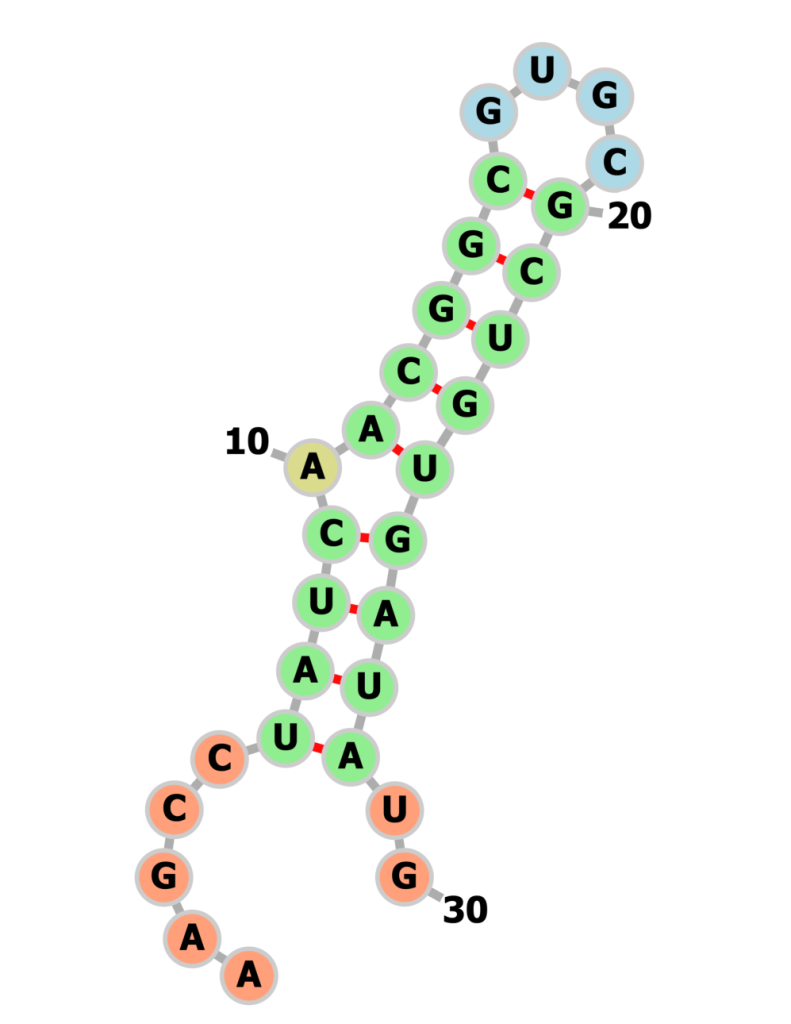
このように! 量子コンピュータ上でmRNAの配列の二次構造を予測することができたのである!
一番長いものでは、
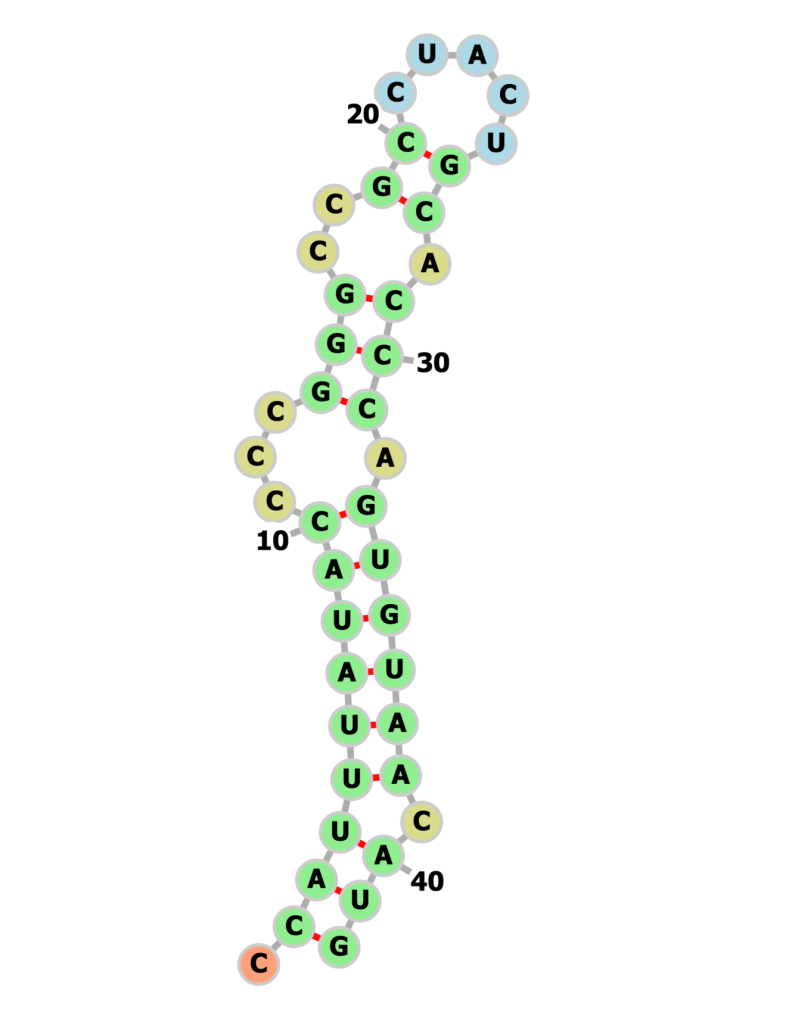
と、42塩基長のmRNAの二次構造を予測できている(ただしこれについてはハードウェア上での回路最適化は行っていない)。
割と単純な構造だけが論文中では図になっているが、他にもRNAは様々な構造を取りうるため、そうした構造まで推定できるのかどうかは疑問が残る。
量子コンピュータでの実現可能性
フォールトトレラントな量子コンピュータ(FTQCのような)ではリソースのスケーリングを比較的簡単に導出できるが、今回のような変分量子固有値ソルバー(VQE)(やQAOA)を使用するようなケースではスケーリングを予測することは困難であるとされる(Scriva et al., 2024)。ただ古典コンピュータを用いた計算にも配列長の限界が存在するため、量子ハードウエアと併用することでより最適な結果を導くことができる可能性がある。
結論と展望
本研究では、量子コンピュータを用いてRNA配列の二次構造予測に基づく最適化問題を解く実現可能性を検討した(いわゆるフィジビリティスタディ)。結果として、ノイズの多い量子ハードウェア上で適切なキャリブレーションと標準的なエラー軽減を行うことで、CVaR-VQEのような最適化スキームが比較的大きな問題インスタンスに対しても十分に信頼性のある出力を生成できることが示された。
しかし、100量子ビットを超える問題サイズに対するこれらの方法のスケーラビリティは、まだ検討の余地がある。量子ハードウェアが進化するにつれて、アルゴリズム技術の改善が最適化のための量子コンピュータの利用見通しはどんどん強化していくだろうと著者等は述べている。この研究は、主に実用規模の量子ハードウェアの能力に焦点を当て、利用可能な量子アプローチの一部のみを考慮したが、将来の研究ではより高度な最適化技術を探求する予定だという。
本研究の結果は、量子コンピューティングがRNAの折り畳み機構に関して、迅速な二次構造の推定を可能にすることを示している。
さいごに
arXivに論文が出てからずっとタブに入れて読もう読もうと寝かせていたが、こうして記事を書きながら読むことで少し量子コンピュータに対する理解が深まったと感じている。まだよくわからないところが多いのでもし誤りや勘違いがあったらコメントで指摘していただけると嬉しいです。
私(生物学者)がなぜ量子コンピュータにこだわるのか問われたことがあるが、1982年、ファインマンという著名な物理学者(「ファインマン物理学」という教科書でおなじみの)はこう言い残している。
If you want to make a simulation of nature, you’d better make it quantum mechanical, and by golly it’s a wonderful problem, because it doesn’t look so easy.
Feynman, R.P. Simulating physics with computers. Int J Theor Phys 21, 467–488 (1982). https://doi.org/10.1007/BF02650179
「自然をシミュレーションしたければ、量子力学の原理でコンピュータを作ったほうがいい」
生物の進化の原動力は突然変異であり、以前の記事にも触れたがその突然変異は量子効果が関わっている。今回のような量子コンピュータによる自然の模倣の研究は、いずれ我々地球生命体の進化の根源の理解に繋がるであろう。
参考文献
- Alevras, D., Metkar, M., Yamamoto, T., Kumar, V., Friedhoff, T., Park, J. E., … & Galda, A. (2024). mRNA secondary structure prediction using utility-scale quantum computers. arXiv preprint arXiv:2405.20328.
- Zhao, Q., Zhao, Z., Fan, X., Yuan, Z., Mao, Q., & Yao, Y. (2021). Review of machine learning methods for RNA secondary structure prediction. PLoS computational biology, 17(8), e1009291.
- Sato, K., Akiyama, M., & Sakakibara, Y. (2021). RNA secondary structure prediction using deep learning with thermodynamic integration. Nature communications, 12(1), 941.
- Zuker, M. (1989a). [20] Computer prediction of RNA structure. In Methods in enzymology (Vol. 180, pp. 262-288). Academic Press.
- Zuker, M. (1989b). On finding all suboptimal foldings of an RNA molecule. Science, 244(4900), 48-52.
- Zakov, S., Goldberg, Y., Elhadad, M., & Ziv-Ukelson, M. (2011). Rich parameterization improves RNA structure prediction. Journal of Computational Biology, 18(11), 1525-1542.
- Szikszai, M., Wise, M., Datta, A., Ward, M., & Mathews, D. H. (2022). Deep learning models for RNA secondary structure prediction (probably) do not generalize across families. Bioinformatics, 38(16), 3892-3899.
- Lyngsø, R. B., & Pedersen, C. N. (2000). RNA pseudoknot prediction in energy-based models. Journal of computational biology, 7(3-4), 409-427.
- Fox, D. M., MacDermaid, C. M., Schreij, A. M., Zwierzyna, M., & Walker, R. C. (2022). RNA folding using quantum computers. PLOS Computational Biology, 18(4), e1010032.
- Jiang, J., Yan, Q., Li, Y., Lu, M., Cui, Z., Dou, M., … & Guo, G. P. (2023). Predicting RNA Secondary Structure on Universal Quantum Computer. arXiv preprint arXiv:2305.09561.
- Kim, Y., Eddins, A., Anand, S., Wei, K. X., Van Den Berg, E., Rosenblatt, S., … & Kandala, A. (2023). Evidence for the utility of quantum computing before fault tolerance. Nature, 618(7965), 500-505.
- Barkoutsos, P. K., Nannicini, G., Robert, A., Tavernelli, I., & Woerner, S. (2020). Improving variational quantum optimization using CVaR. Quantum, 4, 256.
- Nakanishi, K. M., Fujii, K., & Todo, S. (2020). Sequential minimal optimization for quantum-classical hybrid algorithms. Physical Review Research, 2(4), 043158.
- Oliv, M., Matic, A., Messerer, T., & Lorenz, J. M. (2022). Evaluating the impact of noise on the performance of the variational quantum eigensolver. arXiv preprint arXiv:2209.12803.
- Vicens, Q., & Kieft, J. S. (2022). Thoughts on how to think (and talk) about RNA structure. Proceedings of the National Academy of Sciences, 119(17), e2112677119.
- Zaborniak, T., Giraldo, J., Müller, H., Jabbari, H., & Stege, U. (2022, September). A QUBO model of the RNA folding problem optimized by variational hybrid quantum annealing. In 2022 IEEE International Conference on Quantum Computing and Engineering (QCE) (pp. 174-185). IEEE.
- Nussinov, R., & Jacobson, A. B. (1980). Fast algorithm for predicting the secondary structure of single-stranded RNA. Proceedings of the National Academy of Sciences, 77(11), 6309-6313.
- Mathews, D. H., Sabina, J., Zuker, M., & Turner, D. H. (1999). Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. Journal of molecular biology, 288(5), 911-940.
- Robert, A., Barkoutsos, P. K., Woerner, S., & Tavernelli, I. (2021). Resource-efficient quantum algorithm for protein folding. npj Quantum Information, 7(1), 38.
- Lavrijsen, W., Tudor, A., Müller, J., Iancu, C., & De Jong, W. (2020, October). Classical optimizers for noisy intermediate-scale quantum devices. In 2020 IEEE international conference on quantum computing and engineering (QCE) (pp. 267-277). IEEE.
- Pellow-Jarman, A., McFarthing, S., Sinayskiy, I., Pillay, A., & Petruccione, F. (2023). QAOA Performance in noisy devices: the effect of classical optimizers and ansatz depth. arXiv preprint arXiv:2307.10149.
- Vidal, G. (2003). Efficient classical simulation of slightly entangled quantum computations. Physical review letters, 91(14), 147902.
- McKay, D. C., Hincks, I., Pritchett, E. J., Carroll, M., Govia, L. C., & Merkel, S. T. (2023). Benchmarking quantum processor performance at scale. arXiv preprint arXiv:2311.05933.
- Scriva, G., Astrakhantsev, N., Pilati, S., & Mazzola, G. (2024). Challenges of variational quantum optimization with measurement shot noise. Physical Review A, 109(3), 032408.





![【Qiskit】マルチオミクス解析を量子機械学習でやる①[環境構築・基礎]](https://kimbio.info/wp-content/uploads/2024/05/2203027-100x100.jpg)