分子系統樹を作成する時、特に何も考えずにツールに突っ込んで得られたデータの樹形を見ているということはないだろうか？
系統樹に関する既知の問題点として「Long branch attraction」という現象が古くから(50年くらい前)知られている。ロングブランチアトラクション、の日本語訳はまだ当てられていないが、「長い枝の引力」というところだろうか。文字通り、長い枝に引き寄せられて誤った樹形を推定してしまう現象である。
分子系統樹を書く際にはぜひとも頭に入れて考慮すべき問題であり、今回はそれについて記事を書いていく。
Long branch attraction とは？
端的に言うと、「進化速度が大きく異なるような種を含むデータセットを元に系統樹を推定した時、その進化速度の違い故に誤ったクレード(系統群)を作ってしまう」という現象のことである。進化速度が速いと系統樹の”枝の長さ”が長くなることからこの Long branch attraction の名前がつけられた。
何が系統樹に影響を及ぼしているのかというところだが、1つの例として収斂(しゅうれん)進化が挙げられる。「系統独立的に」偶然似たような配列になってしまったような場合、同じクレードにそれらが入ってしまうということである。系統樹推定のアルゴリズム的には、その偶然の同じ変異が共通祖先において一度生じた変異を引き継いでいるものと誤って推定してしまう。
分子系統解析におけるこの手の収斂はどうしようもない。塩基は4種類しかないし、アミノ酸ですら20種類しかない、そもそも配列の長さも有限だからだ。どうしても進化速度が速い、つまり置換が多く溜まっている場合似たような配列に”収斂”してしまう。
具体的な系統樹の例として、以下の図のような「誤った推定」が起きることがある(Brahme, 2014)。
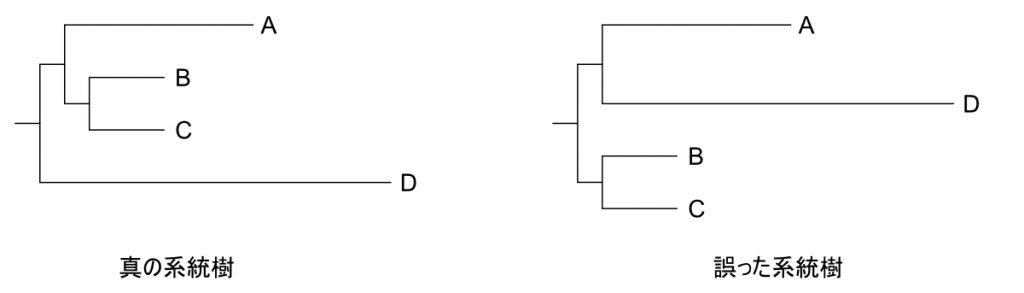
また、Long branch attractionの定義についてBergstan (2005)では以下のように(過去の文献を引用しながら)述べている。
「長い枝と短い枝の組み合わせにより、有限のデータセット(分析対象)に偏りが生じたり、統計的不整合が生じたりする状況」(Sanderson, 2000)
「収束的または並行的な変化による類似性が、推定手順に内在するバイアスのために、分類群の人工的なグループ化を引き起こすあらゆる状況」(Anderson, 2004)
より具体的な計算例
この Long Branch Attraction は最大節約法(maximum parsimony method)によって引き起こされることが多いと言われている(Brahme, 2014)。
では具体的例を取り上げて実際に計算してみよう。以下のような系統的に離れた生物A-Dの真の系統樹と配列があったとき、最大節約法を考える(Kapli et al., 2021)。Dはアウトグループとして用いる。また、生物Bと生物Dは進化速度が速いことで知られている。
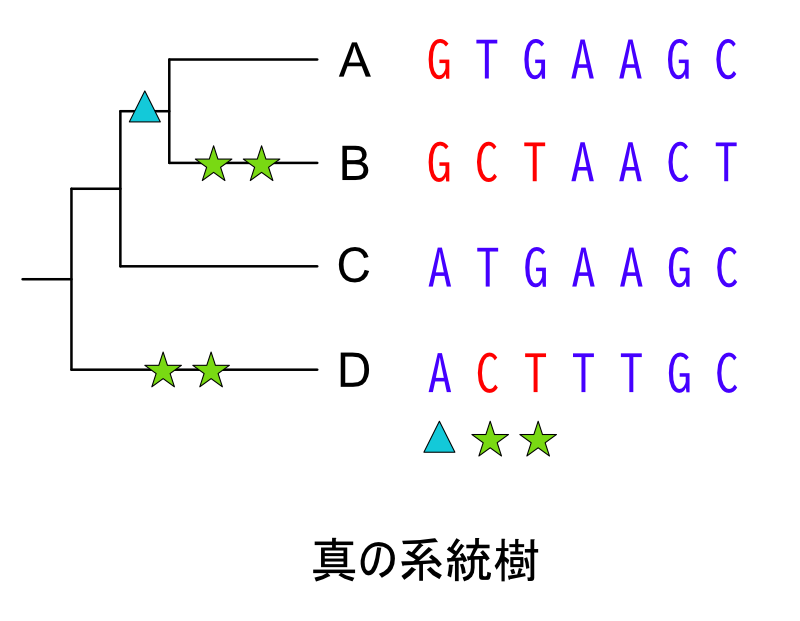
ここで、Parsimony Informative site について考える。Parsimony Informative site とは、ある2種類以上の多型が存在するサイトかつそれらの最小出現頻度が少なくとも2以上であるサイトを指す。上図では三角と星が下についているサイトがそれに相当する。星が2つ並んでいるサイトは生物B,Dにおいて独立に変異を獲得し、収斂が起きているサイトである。
次に、系統樹上で置換数に応じた樹形を推定してみる。我々は上の「真の系統樹」を知っているが、通常系統樹を推定するときは真の系統樹は知らない。まずは5つの置換が生じたと仮定した場合を考える。
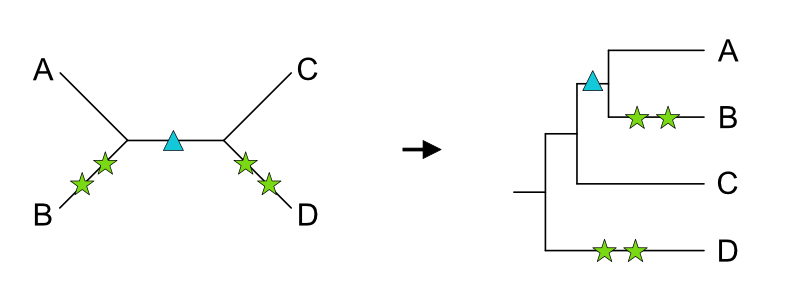
左の無根系統樹から有根系統樹を考えると生物Dをアウトグループに取る時、右のようになる。これは「真の系統樹」と一致した系統樹となる。
ただ、最大節約法で重要な考えは「考えうる最小の変異」であるため、ここから更に系統樹上に“落ちる”変異を少なくして考えてみる必要がある。では4つの場合(最節約的)はどうだろうか。
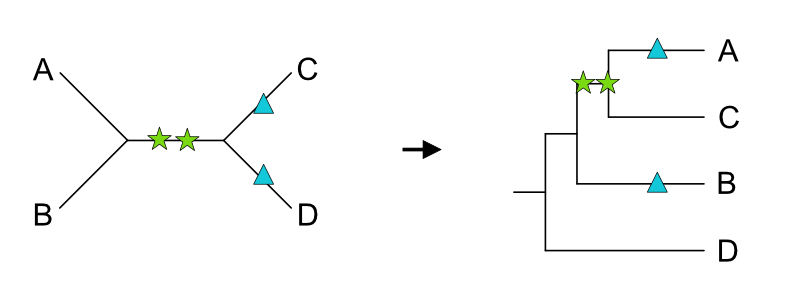
ご覧のように、誤った系統樹を導き出してしまう。進化速度が速い生物B,Dで独立に収斂的に獲得した2つの同じサイトの変異が最大節約法では独立に起きたとはみなさず異なる枝上で起きたと推定する。Long Branch Attraction である。
対処法
このようなことが起きてしまうと、求めている正しい系統樹が出力されず、誤った結論を導き出してしまいかねない。そこで Long Branch Attraction を避けるためには様々な方法が考案されてきている。
例えばそもそもその長い枝の葉(遺伝子、種など)を取り除いてしまうというのが1つの手だ。その他には最尤法やベイズ方などの Long Branch Attraction が少ない傾向にあるアルゴリズムを使用するという手もある(Bergsten, 2005)。昔こそ NJ/ML/Bayesian みたいに3つ推定値を出したりとかしていたがコンピュータが発達した今は専ら最尤法が使われているのではないだろうか。
その他にはSAW メソッド(Siddall and Whiting, 1999)なるものがあって、分類群Aと分類群Bが存在し、それらが Long Branch Attraction であることが考えられる時、片方ずつ削除してそれぞれの分岐の位置を確かめる。もし一致しないのであれば Long Branch Attraction である可能性が高い、というものだ。
Bootstrap 法は現在ではよく使われる手法だが、 Long Branch Attraction を完全に防ぐことはできないようである(Brahme, 2014)。
その他にも塩基配列の場合のみに適用できるが、コドンの3つ目は置換速度が1つ目2つ目よりも速い(縮重による)。そのため、遺伝子配列をアライメントした時、コドンの3つ目と1,2つ目を分けて計算するというやり方もあるようだ(Kapli et al., 2021を参照してほしい)。
さいごに
配列をツールに突っ込んで出てきたものを脳死で眺めるだけでなく、一度じっくり「本当にこれが正しいのか？」と疑問を持ち、必要があれば「葉」や「枝」を削ったり増やしたりして Long Branch Attraction が生じていないかどうかを検証するようにしたほうがいいだろう。
参考文献リスト
- Brahme, A. (2014). Comprehensive biomedical physics. Newnes.
- Bergsten, J. (2005). A review of long‐branch attraction. Cladistics, 21(2), 163-193.
- Sanderson, M. J., Wojciechowski, M. F., Hu, J. M., Khan, T. S., & Brady, S. G. (2000). Error, bias, and long-branch attraction in data for two chloroplast photosystem genes in seed plants. Molecular Biology and Evolution, 17(5), 782-797.
- Anderson, F. E., & Swofford, D. L. (2004). Should we be worried about long-branch attraction in real data sets? Investigations using metazoan 18S rDNA. Molecular phylogenetics and evolution, 33(2), 440-451.
- Kapli, P., Flouri, T., & Telford, M. J. (2021). Systematic errors in phylogenetic trees. Current Biology, 31(2), R59-R64.
- Siddall, M. E., & Whiting, M. F. (1999). Long‐branch abstractions. Cladistics, 15(1), 9-24.
