- 2020/10/15 不適当な説明を修正
- 2020/11/16 微妙な表現を修正
- 2025/02/04 LaTeXの表現を修正
はじめに(人間のはなし)
日本に関わらず世界において,近親相姦・近親婚はタブー視されている.
例えば日本では,近親相姦や近親間での事実婚は法律上阻害されるようなことはないが,婚姻届を出すことができない.親子,きょうだい,”おじ”と”めい”などがそれに当たる.
ではなぜそれが”タブー視”されるのであろうか.
グッピーやエビなども近親交配を繰り返していると段々と弱くなっていったり奇形や不妊の個体が生じる確率が高くなることはよく知られている.ヒトにおいてもハプスブルク家の近縁の婚姻によって血友病が広まり,滅亡したという話は聞いたこともあるだろう.
そうした疾患の背景には“遺伝子”が強く関与している.
自分の祖先の数は無限大?
遺伝子の話に入る前に,まずは「共通祖先」の話をしておきたい.
人間には当然(生死は問わず)両親がおり,そしてその両親にもそれぞれ両親が存在する.つまりあなたの祖父母に当たる存在だ.当然その祖父母にもそれぞれ両親がいる……と考えていくと,世代を1つ遡るごとに祖先の数は指数関数的に増大する.つまり,n世代前の祖先の数は\(2^ n\)ということになる.
人間が1世代20年で交代すると仮定すると,100年で5世代,つまり\(2^{5} = 32\)人の祖先がいた,ということになる.これをどんどんスケールアップして1000年前を考えてみると,50世代,つまり\(2^{50} \simeq 1,000,000,000,000,000\) 人も祖先がいた,ということになる.1000兆人.すごい,すごいじゃん1019年の日本の人口,今の世界人口を超えている! ということになってしまう.
が,当然ながらそんなことはありえない.
ではどうしてそうならないか,という話だが,どこかで必ず祖先を共有している,ということである.イメージとしては下の図のようなものだ.

つまり,祖先は必ずどこかで共有している,といっても良いだろう.隣の彼や彼女と遠い祖先を共有している……と考えるとなんだか不思議な気持ちにならないだろうか.私はならない.
祖先を共有する確率を求める方法を後ほど紹介する.
遺伝子がどう遺伝するかを考える
さて,祖先が共有しているという話に続いて今度は遺伝子というものがどう祖先から子孫へと受け継がれていくのだろうか,ということについて考える.
ここから先はすべて二倍体生物として扱う.二倍体生物とは,ようは同じ染色体を2つ持つ生物,ということである.我々人間は染色体を23対持っている(性染色体を含む).同じ染色体を持っている,ということは基本的には同じ遺伝子を2つ持っているということである.遺伝子とか染色体がよくわからないという人は 遺伝子とは染色体上に乗っている領域,としてひとまず考えて欲しい.
この染色体は精子・卵が作られるときに減数分裂によってランダムに1本だけ配偶子(精子・卵)に受け継がれる.
本当は稀にランダムに1本だけ,ではなく2本誤って受け継がれてしまうなどエラーが生じる場合があるが,今回の話に限っては上記の通り2本のうち1本だけ子孫に受け継がれるということを前提条件としておく.
次にアレル(対立遺伝子)という用語も軽く触れておく.アレルとは簡単に言うとこの2本の染色体上の同じ”位置(遺伝子座)”に存在する2つの遺伝子のことである.遺伝学を高校で習った人だと「AA」「Aa」「aa」などといった遺伝子型の表記を見たことがあると思うが,このAとかaがアレルの表記である.そしてAAやAaといった一個体が持つアレルを表したものが遺伝子型である.
かなりざっくり言うと,2本の染色体を比べた際に同じ場所に存在している塩基配列が異なるとそれは別のアレルである,といった感じである.
今回は基本的に突然変異が入る確率というものを無視して考える.
近交係数を考える
次に集団遺伝学という学問の一分野における「近交係数(inbreeding coefficient) \(F\)」というものについて考える.難しい話を抜きにしたいという人はこの節ともう1つ先の節を飛ばしてほしい.
近交係数\(F\)とは,ある個体が持つ2つのアレルが共通祖先由来であるがために同じアレルである,という確率のことである.
この「 2つのアレルが共通祖先由来であるがために同じアレルである」ということを同祖(identity by decent, IBD)という.
さらに一般的に,集団内に存在するアレルから2つ選んだ任意のアレルの組み合わせのうち,同祖(IBD)である確率,とも定義される.
ここでいう「集団」というものは,互いに交配を行う生物集団のことを指す.
さて,難しそうな定義を延々と述べていてもわからないと思うので,具体的なケースを取り上げてこの近交係数への理解を深めることとしよう.
いとこ婚をした場合の子供における近交係数
いとこ婚を考えてみる.

□は男を,○は女を示す.それぞれの□○の中の丸はアレルを示す.
共通祖先(世代A)から生まれた子供からさらに生まれた子供(世代C)同士が交配した場合,世代Dにおける子供が持つ2つのアレルが同じである確率を考える.
まず1つのアレルについて考える.図2の黒丸(●)を見て欲しい.共通祖先(世代A)のうち,母親側がもともとは持っていたアレルである.それが息子・娘に伝わる確率がそれぞれ\(\frac{1}{2}\)ずつ,さらにそれが世代Cの子供に伝わる確率が\(\frac{1}{2}\)であり,それがさらに世代Dの子供に伝わる確率も\(\frac{1}{2}\)である.
つまり,黒丸が世代Aの母親から世代Dの子供に左右の経路を通って伝わる確率はそれぞれ
\[ \left(\frac{1}{2}\right)^3 \]
であるため,世代Dの子供がその両方を持つ確率は
\[ \left(\frac{1}{2}\right)^3 \times \left(\frac{1}{2}\right)^3 \] である.
これがそれぞれ世代Aの4つのアレルについて考えられるため,求める近交係数\(F\)は,
\[ F = \left(\frac{1}{2}\right)^6 \times 4 = \frac{1}{16} \]
となる.
親子同士の近交係数
次に親子において同じアレルを持つ確率を考える.今回も黒丸のアレルに着目する.
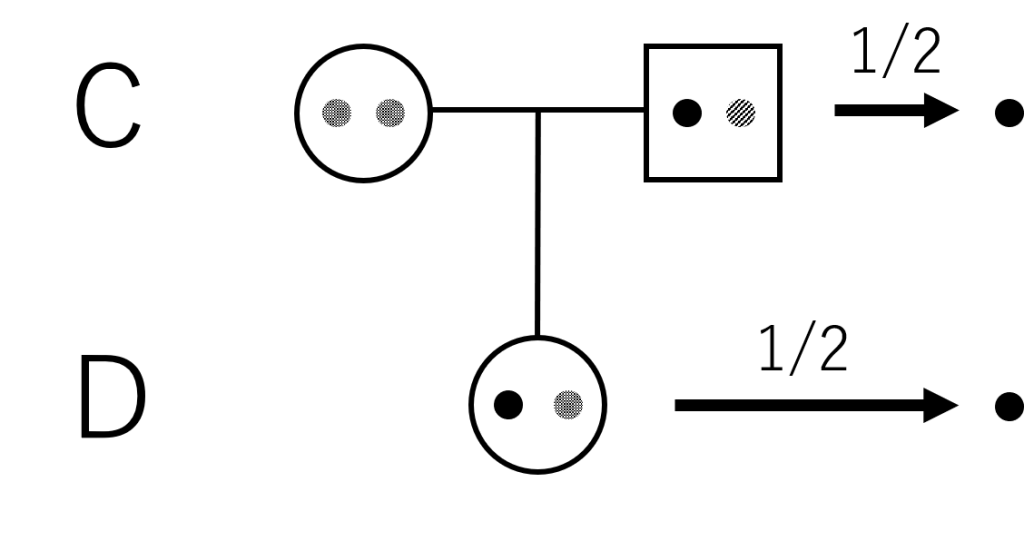
図3のように,黒丸のアレルを選び出す確率はそれぞれ1/2であるため,親子同士の近交係数\(F\)は$$\frac{1}{2} \times \frac{1}{2} = \frac{1}{4}$$となる.
いとこ同士の近交係数
話を少し戻して先程の世代Cのいとこ同士の近交係数を求める.
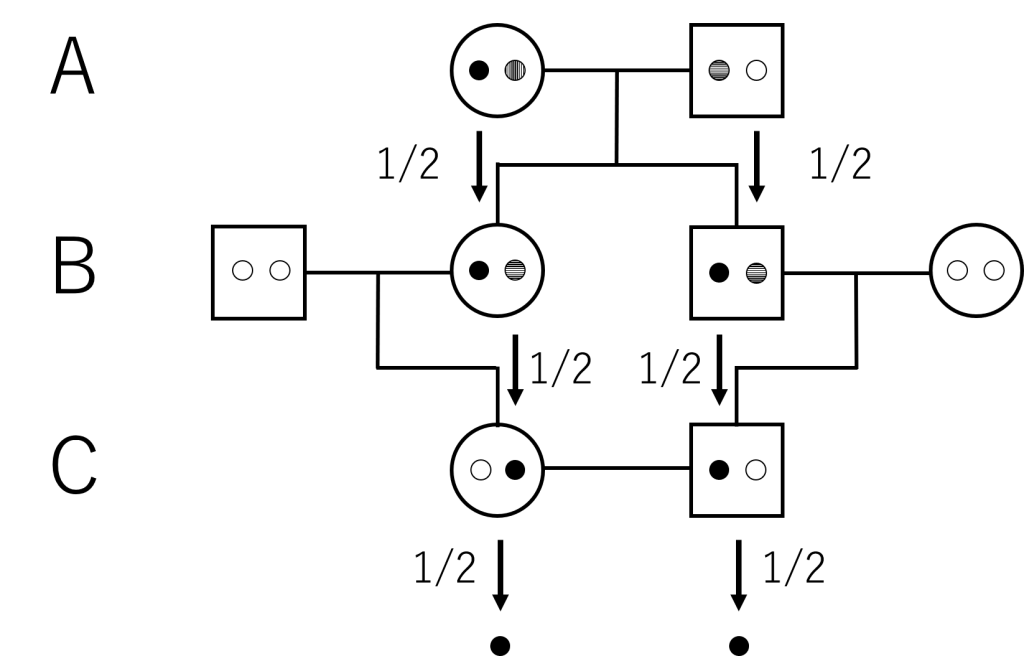
黒丸アレルを同様に考えると,世代Cのそれぞれの個体に黒丸アレルが伝わる確率はそれぞれ$$\left(\frac{1}{2}\right)^2$$である.さらにその世代Cの個体が持つ2つのアレルのうち,黒丸アレルである確率というものは1/2である.
つまり,世代Cのそれぞれの個体からアレルを1つ取り出したとき,それが黒丸である確率というものは$$\left(\frac{1}{2}\right)^3$$である.
世代Aの4種類のアレルについて考えると,求める近交係数は
$$F = \left(\frac{1}{2}\right)^3 \times \left(\frac{1}{2}\right)^3 \times 4 = \frac{1}{16}$$
となる.
戻し交配の近交係数(2019/10/09追記)
質問が来ていたので追記しておく。戻し交配を行った際のその子供の近交係数を求めたい。以下のような図の交配が考えられる。
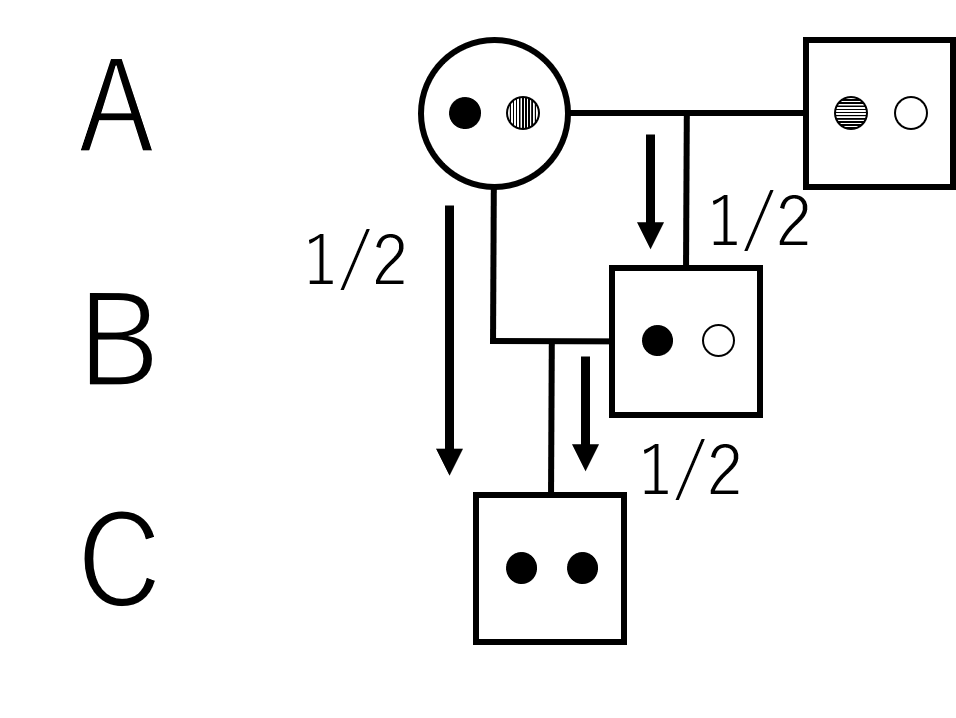
つまり、求める近交係数は
$$ F = \left (\frac{1}{2} \right) \times \left (\frac{1}{2} \right) ^2 = \left (\frac{1}{2} \right) ^3$$
である。
近交係数を一般化する
さて,ここまで話を3つについて書いてきたが,より一般化したいと思う.個別のケースばかりに着目していても集団とか,より多くの世代について考える際にいちいち計算していてはきりがない.
今回はライト-フィッシャー集団というモデルで考えていく.ざっくり説明すると集団サイズ\(N\)の個体からランダムに2個体選び出し,さらにそれぞれからアレルを1つずつ取り出し,そこから次世代の子孫の遺伝子型を決める.これを\(N\)回繰り返す,といった操作からなる集団のことである.
さて,ここに集団サイズ\(N\)の二倍体集団があり,その\(t\)世代目における任意の個体における近交係数\(F_t\)を求めたい.
考え方としては,世代\(t-1\)における“個体”という概念を取っ払ってその集団における”アレル”のみについて着目する.このある集団における遺伝子の集合のことを遺伝子プール(gene pool)という.
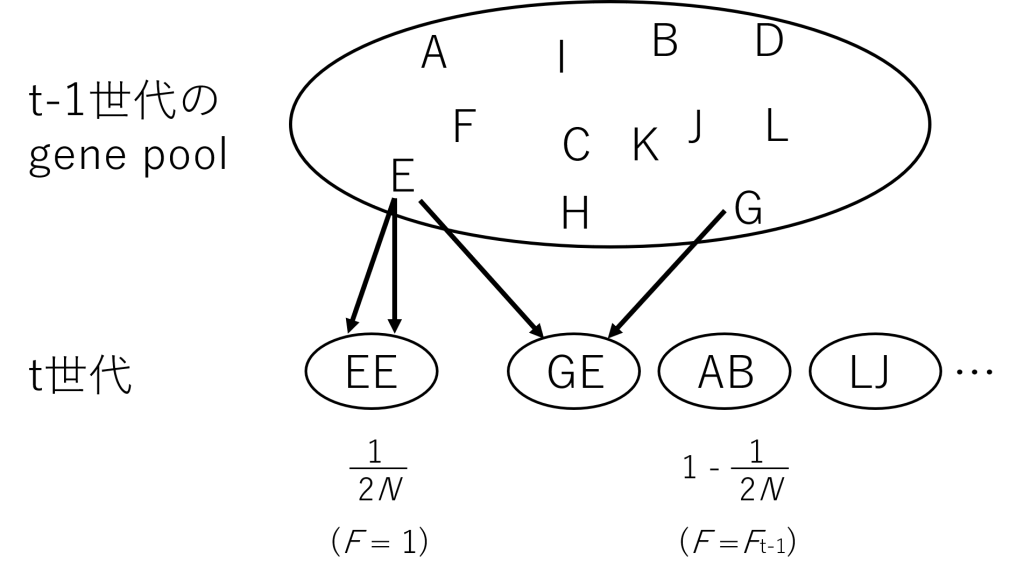
アルファベットはそれぞれアレルを表している.
図5に即して考えていく.ここからまずアレルEを取り出す(図5 t世代の一番左の個体).次に重複を許して1つアレルを選びだしたとき,\(\frac{1}{2N}\)の確率で同一のアレルEを選ぶことになる(\(F=1\)).
また,ある個体が遺伝子型EEではない確率というものは,遺伝子型EEになる余事象の確率であるため,$$1-\left(\frac{1}{2N}\right)$$である.その中で2つのアレルが同じとなる確率は\(t-1\)世代の近交係数\(F_{t-1}\)に依存するため,求める\(t\)世代目における近交係数\(F\)は,
$$ F_{t} = \frac{1}{2N} + \left( 1-\frac{1}{2N}\right)F_{t-1}$$
となる.
式(1)を変形すると,
$$ 1-F_{t} = (1-F_{0})\left( 1-\frac{1}{2N}\right)^t$$
となり,さらにこの式は
$$ (1-F_{0})e^{-\frac{t}{2N}} $$
というように近似できる.\(F_0\)は初期状態の\(F\)である.
この式から,近交係数というものは時間が増加するに連れて増加する,つまり時間が経てば立つほど共通祖先を持つ確率というものが高くなるということがわかる.
近交係数から近親交配を考える
近親交配をきょうだいなどと交配するということのみならず,拡大解釈して「小さなサイズの集団内での交配」と考えることとする.
よく世界史などでは「血統」などが重視され,その血筋のある親戚同士が交配する,といったことが見られる.これも「血筋同士」という小さい個体サイズの集団内での交配として見ることができる.
さて,式(1)と(2)を見てほしいのだが,この式は集団サイズ\(N\)の値に依存している.
つまり,集団サイズ\(N\)が減少すると近交係数は上昇,つまり\(t\)世代さかのぼった際にIBDである確率というものが上昇する.
ここでIBDによる弊害について考える.例えば図2のようにアレルが遺伝するとき,例えば黒丸アレルが潜性(劣性)遺伝子であり,ホモ接合となったとき有害であることを考える.ホモ接合とは図2のD世代の個体のように2つアレルが同一のものであることをいう.この遺伝子はヘテロ接合(黒丸と黒丸以外)の場合は病気を引き起こさない.

通常顕性であるような有害な変異は集団どころか個体にとって有害であるため集団中からすぐに取り除かれることが多い.しかし「潜性かつヘテロではその個体の生存率に影響を及ぼさない変異」であった場合,集団中に”残ってしまう”ことがある.ただ,その変異の割合が小さいような大きな集団である場合,ホモで持つことになる確率は小さくなる.
しかし近親婚を繰り返していくと,あるアレルについてホモで持つ確率が高くなる.すなわち有害なアレルをホモで持つ可能性も高くなるため,生存率に影響を与えていくこととなる.
このことは経験則からわかっていたのか,少なからぬ地域で近親婚がタブーになっていた,というわけだ.
しかし逆に言えば,「人間が欲する形質に関与する遺伝子」をホモで持った個体を作り出して理想の形質をもった個体を得たいようなときは,このように近い血縁関係にあるもの同士を掛け合わせる事が多い.それがペットなどの品種に用いられている.もちろん,その遺伝子の影に何らかの”疾患遺伝子”が連鎖している可能性も捨てきれないのだが.
おわりに
もちろんこの有害な変異についてはホモ接合によるもの以外にも要因があるため今回の説明が全てというわけではない.
近親交配がタブーとされている所以には今回説明したように「血が濃くなる」,つまり同じ変異遺伝子をホモで持つ確率が高くなることが関係している.
参考文献
- 長田直樹(2019) 『進化で読み解く バイオインフォマティクス入門』 pp33-41
――バイオインフォマティクスの基礎となる集団遺伝学について導入からしっかりと書かれている良書.Amazonで購入 - Conservation genetics

![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/0a9ad1ee.364401d8.0a9ad1ef.5ac65ebb/?me_id=1213310&item_id=19600126&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F1419%2F9784627261419.jpg%3F_ex%3D240x240&s=240x240&t=picttext)





![【Qiskit】マルチオミクス解析を量子機械学習でやる①[環境構築・基礎]](https://kimbio.info/wp-content/uploads/2024/05/2203027-100x100.jpg)


ピンバック:ヒトと他の動物は交尾し、子孫を残せるのか - Kim Biology & Informatics
ピンバック:なぜ動物の交尾はバックばかり?~魚の妊娠の起源から陸上四肢動物まで~ - Kim Biology & Informatics
ピンバック:氷漬けマンモスのDNAから絶滅した原因を明らかに – 最後のマンモスは花の匂いを嗅げなかった? – Kim Biology & Informatics