【Qiskit】Qiskit-aer で量子回路シミュレーション – ベル状態

前回は量子コンピュータに実際にジョブを投げて実行結果を取得したが、毎回3時間も待たされていては貴重な余暇がもったいない。そこで、量子回路シミュレータを用いてQiskitを使った疑似量子計算を行う。今回はそのライブラリのひとつ、Qiskit-aer について紹介する。

Qiskit-aer のインストール

pip install qiskit-aer

ちなみにQiskit-aerはGPUにも対応しており、CUDAに対応したグラボならGPUでシミュレートできる。その場合、

pip install qiskit-aer-gpu

でインストールできる。

ベル状態の生成

量子回路シミュレータでベル状態を生成してみる。

ベル状態 (Bell state) とは2つの量子ビットが絡み合った状態のことである。厳密にはただ絡み合った、というよりは $| 0 \rangle$ と $| 1 \rangle$ がそれぞれ理論上50%の確率で観測されるような状態のことを指す。

量子計算において重要な操作のひとつにアダマール変換 (Hadamard transformation) というものが存在する。アダマール変換を行う量子ゲート、アダマールゲート $H$ は量子回路上では以下のような図で示される。

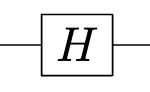
行列表現は次式で表される。

$H = \frac{1}{\sqrt{2}}\begin{pmatrix}1 & 1 \\1 & -1 \end{pmatrix}$

また、基底状態 $| 0 \rangle$ と $| 1 \rangle$ に対して作用する式は

$H|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)$

$H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)$

で表される。

さらにこれにCNOTゲート(CXゲートとも表記する)を作用させるような量子回路を考える。

この図中の+で示されているところがCNOTゲートになる。

$|\psi\rangle = |00\rangle$

と量子ビットを初期化した状態から、アダマールゲートを作用させると

$|\psi\rangle = \frac{1}{\sqrt{2}} (|0\rangle + |1\rangle) \otimes |0\rangle = \frac{1}{\sqrt{2}} (|00\rangle + |10\rangle)$

となる。さらにこれにCNOTゲートを作用させると、

$|\psi\rangle = \frac{1}{\sqrt{2}} (|00\rangle + |11\rangle)$

という状態が得られる。これがベル状態であり、もつれを表している。量子力学で必ず学ぶベルの不等式で有名なJohn Stewart Bellにちなんでいる。

(自分の整理のための)前置きが長くなったが、これをQiskit-aerで量子回路シミュレートしてやる。

from qiskit_aer.primitives import Sampler
from qiskit import QuantumCircuit
from qiskit.visualization import plot_histogram

# ベル状態を生成する量子回路
bell = QuantumCircuit(2)
bell.h(0)         # 量子ビット0にアダマールゲートを適用
bell.cx(0, 1)     # 量子ビット0と量子ビット1の間にCNOTゲートを適用
bell.measure_all() # すべての量子ビットを測定
 
# 量子回路の実行
quasi_dists = Sampler().run(bell, shots=1000).result().quasi_dists[0]

# 結果の表示
print(quasi_dists)

これは自分のコンピュータ上で行われる計算なので、すぐに結果が出てくる。