今回は量子コンピュータが生命科学にどういう形でアプローチできるのか、最近(2022年)のレビューを通じて紹介したい。量子コンピュータに限らず、現在の動向を色々と抑えて書き留めたいと思う。
最近の計算生命科学(バイオインフォ)の動向
最近のバイオインフォマティクスの分野の発展は著しい。特にタンパク質の立体構造推定の分野において Alphafold2 (Jumper et al., 2021) や RoseTTAFold (Beak et al., 2021) が公開・発表され、タンパク質の予測された立体構造のデータベースが拡充された。
また、「ゲノムをとにかく大量に読む」ということが一般化し、さらにヒト以外の種においてもHiFiやHi-Cなどの技術により染色体レベルでアセンブルされたゲノムも数多く登録されるようになった。2000年代〜2010年代にあったような、「一つの種のゲノムを決定し、Natureなどの総合誌の表紙を飾る」という潮流は過ぎ去り、「大量の種のゲノムを決定したうえで大規模解析を行った」ような論文がNCSなどの総合誌にやっと載るような時代になり、ゲノムが決定されてもそれに付随する論文が(すぐには)発表すらされないような現状である。トランスクリプトーム、RNA-seqのデータも大量に登録されるようになり、こうした塩基配列の情報は公開データベースを通じて誰でも無料で手に入るような時代になった。バイオインフォにおける「ビッグデータ」時代の到来である。また、X線、CTスキャン、MRIなどの医療画像データも膨大な量が蓄積されてきている。
こうした大量のデータを前に、実に様々な計算アプローチが開発されている。Marchetti et al. (2022) によると、現在のバイオインフォの分野における計算アプローチは大きく4つに分類できるという。
配列解析アルゴリズム
オミクスによるDNA、RNA、アミノ酸配列を解析するためのアルゴリズム。次世代シーケンサの低価格化によって遺伝子発現解析が容易になったほか、MSなどによりアミノ酸配列が得られるようになった。それらの配列をゲノム配列にマッピングすることで発現動態を見たり、異なるサンプル間で比較したりするなど(発現変動解析など)の方法が発達している。
構造・機能予測アルゴリズム
塩基配列、アミノ酸配列からタンパク質やRNAの三次元構造予測を行うアルゴリズム。単純に一次配列から三次元構造を予測する先述のAlphafold2のようなもの。また、Gene ontology (遺伝子オントロジー) などによってアノテーションされた情報を利用することで、機能の予測も活発に研究されている。
設計アルゴリズム
バイオテクノロジー、病気の治療用途のために特化した三次元構造をもつタンパク質や生体分子をコンピュータで設計することを目的としたアルゴリズム。例えば、目的の受容体であったり標的分子に対して親和性が高いタンパク質設計が挙げられる (Kuhlman and Bradley, 2019)。
マルチスケールモデリングアルゴリズム
特定の時間スケールにおいて分子システムをモデル化およびシミュレートするためのアルゴリズム。これは原子レベルでの解像度での計算であり、比較的小さな系(原子数十個レベル)が量子力学的にシミュレートできる。量子力学/分子力学 (QM/MM) 手法とも。小さな領域の電子構造の記述(QM)と、それらを取り巻く周囲のタンパク質、溶媒などのMMを組み合わせたもの (Jagger et al., 2020)。
上記に含まれない画像データ解析などもあるが、主に本記事における「バイオインフォマティクス」ではこれらのものを指す。これらの解析は計算量が多いことが課題として挙げられるが、この問題を解決するために「古典コンピュータ(現在我々が使っているコンピュータ)」の代わりに量子コンピュータを使う、あるいは併用するといった研究が進み始めている。
2種類の量子コンピュータ
量子コンピュータの説明に入る前に、軽くその原理について触れておく。「シュレディンガーの猫」とかで聞き馴染みの多い単語だろうが、「重ね合わせ」が量子コンピュータの大きな特徴である。古典コンピュータでは1ビットは「0」「1」のどちらかの状態で表されるが、量子コンピュータでは1ビットを ![]() および
および ![]() の基底状態の正規化された複素係数つきの重ね合わせとして表現することができる。
の基底状態の正規化された複素係数つきの重ね合わせとして表現することができる。
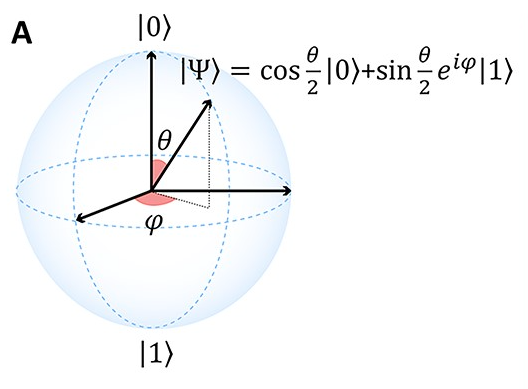
下の図はブロッホ球といって、1量子ビットにおける純粋状態 ![]() を表現したものである。
を表現したものである。
CC-BY-NC 4.0
更に細かい話は割愛するが、量子コンピュータはこの「重ね合わせ」を使うことで、任意の状態の重ね合わせで並列計算ができるというところに強みがあるとされる (Marchetti et al., 2022)。
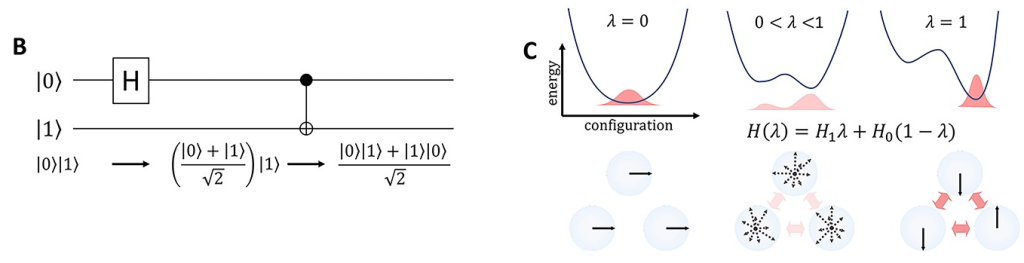
量子コンピュータには大きく「量子ゲート方式」と「量子アニーリング方式」の2つの型に(おおきく言うと)分けられる。これも細かい話はいろんな書籍やサイトで紹介されるので割愛したいが、簡単に言うと、量子ゲート型は一連のプログラム可能な量子ゲート(論理回路)を通じて計算処理をするのに対し(下図B)、量子アニーリング型では量子ゆらぎを利用して最適化問題を解いていくアルゴリズムを採用した方式である(下図C)。生物系の人でアニーリングと聞くとPCRを思い浮かべるだろうが、日本語ではそれと同じ「焼きなまし法」と訳される。
ハードウエアとしては量子ゲート型はエラー訂正に課題があり、量子アニーリング型は既にD-waveなどが実用段階に踏み込んでいるが、いわゆる「万能」ではないので特定の問題を解くのに特化したものではない、というのが現状である。
CC-BY-NC 4.0
理想的には量子ゲート型のコンピュータで量子エラー訂正を備えたフォールトトレラント量子コンピュータ(FTSQ)の実装が挙げられるが、多くの量子ビットが必要なことに加え、量子状態を維持する技術が必要となる。現状それにはまだ遠く、NISQ (Noisy Intermediate-Scale Quantum Computer; ノイズがある中規模の量子コンピュータ) が盛んに開発されているところである。
生命科学における量子計算アプローチ
量子コンピュータを活用したタンパク質の立体構造予測
生命科学における量子計算アプローチの中で特に着目されているのがタンパク質の立体構造の予測である(これは量子化学の分野からのアプローチが大きい)。タンパク質のフォールディング(折りたたみ)は自由エネルギーが最小になる構造になるまでポリペプチド鎖が立体配置空間を探索し続ける段階的なプロセスである。N個のアミノ酸からなるタンパク質は少なくとも![]() 個の三次元構造を取り得ると大まかに推定されている (Englander and Mayne, 2014、この論文のFig.1を見ると想像しやすい)。これは一種の「最適化問題」であるため、量子アニーリングを適応した研究が行われている。
個の三次元構造を取り得ると大まかに推定されている (Englander and Mayne, 2014、この論文のFig.1を見ると想像しやすい)。これは一種の「最適化問題」であるため、量子アニーリングを適応した研究が行われている。
実際に量子アニーリング型の量子コンピュータを使用した研究例では、4つ、8つのアミノ酸配列の相互作用について128量子ビット(実際に利用可能だったのは81量子ビット)のチップ(下の図)を使って解くことが可能であると示している (Perdomo-Ortiz et al., 2012)。

CC-BY-NC-ND 3.0
量子アニーリング型では、ポリペプチド鎖の単純化された格子モデル(タンパク質の構造をアミノ酸の一連の点で表し、それらの点が規則的な三次元格子上に配置されていると仮定するモデル)を使用し、その格子内の各サイトを量子ビットに対応することで最適化問題を解こうとしている。
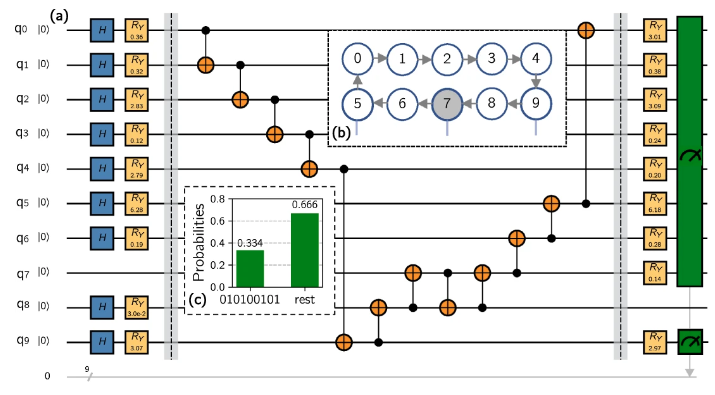
ただやはり量子ビット数の限りがあるために、それほど長いアミノ酸配列には適応できていない。10アミノ酸のペプチドホルモンであるアンジオテンシンの立体構造予測をするために35量子ビットが必要である (Robert et al., 2021)。しかし実際論文中では22量子ビットを使用するように計算上「濃縮」を行っている。これはIBM Q プロセッサの実用上の問題に起因している。ただニューロペプチドである7つのアミノ酸からなるポリペプチド鎖については下図のように9つの量子ゲートを使用して計算を適応し、既知の結果と同じであることを確認している(ベンチマーク)。これはハードの面が大きいため、今後IBMは2025年に4158 量子ビットを目標にしており、今後の量子コンピュータでの適用が期待される。
CC-BY 4.0
これらの量子コンピュータを用いたタンパク質の立体構造予測は統計力学の観点からタンパク質の折り畳みを予測することを目的としている。ただ、最近では何度も紹介しているように Alphafold2 をはじめとした機械学習アルゴリズムに基づく立体構造予測が主流である。この流れを踏まえると、量子機械学習アルゴリズムの開発を通じて量子コンピュータにおけるタンパク質の立体構造予測の開発が進むと期待される (Marchetti et al., 2022)。
ゲノムアセンブリ・アライメントにおける現在のアルゴリズム
冒頭にも述べたように、次世代シーケンサ(NGS)によって大量の塩基配列が取得可能になった。それによりゲノミクス、トランスクリプトミクスをはじめとしたオミクス研究が活発になっている。
このNGSから吐き出されるのはDNA(もしくはRNA)のランダムに断片化されたリードである。そのままでは短くて意味を持たない場合が多いので、「アセンブリ」によってそのリードの断片をつなぎ合わせてより大きな配列を組み上げていく。近年ではロングリードシーケンサ (HiFiやNanopore) の発達によってより長いリードが決定可能になった。
ゲノムが既に決定されている種であれば、NGSを通じて得たDNA・RNA配列の情報をそのゲノムにアライメント(マッピング)することでSNPの検出や発現量の定量などをすることができる。アライメントとは、リファレンスゲノム(参照ゲノム)との間で「最適な一致」を見つける作業である。これについてはある程度効率的なアルゴリズムが開発されているようである (Canzar and Salzberg, 2015)。
一方で、ゲノムを新規にアセンブルする場合 (de novo アセンブリ)、リード間の重複に基づいてコンティグを構築する必要がある。一般的に、ショートリードのアセンブリには de Bruijn graph (DBG) アプローチが、ロングリードのアセンブリには overlap-layout consensus (OLC) アプローチが用いられてきた (Li et al., 2012; Sohn and Nam, 2018)。この2つのアルゴリズムの採用の歴史的経緯は Li et al. (2012) に詳しい。この2つはアルゴリズムの複雑さと計算効率が大きく異なる。OLC アセンブリではそのレイアウトステップがNP困難であることが知られているハミルトン路問題であり、計算が複雑である。現状、ロングリードではそこまで深く読まないのでOLCアルゴリズムを採用してアセンブルすることができる。しかしリード数が増加するとリード間の重複を検索するためのリードのペア比較が計算上のボトルネックになることが言われている。
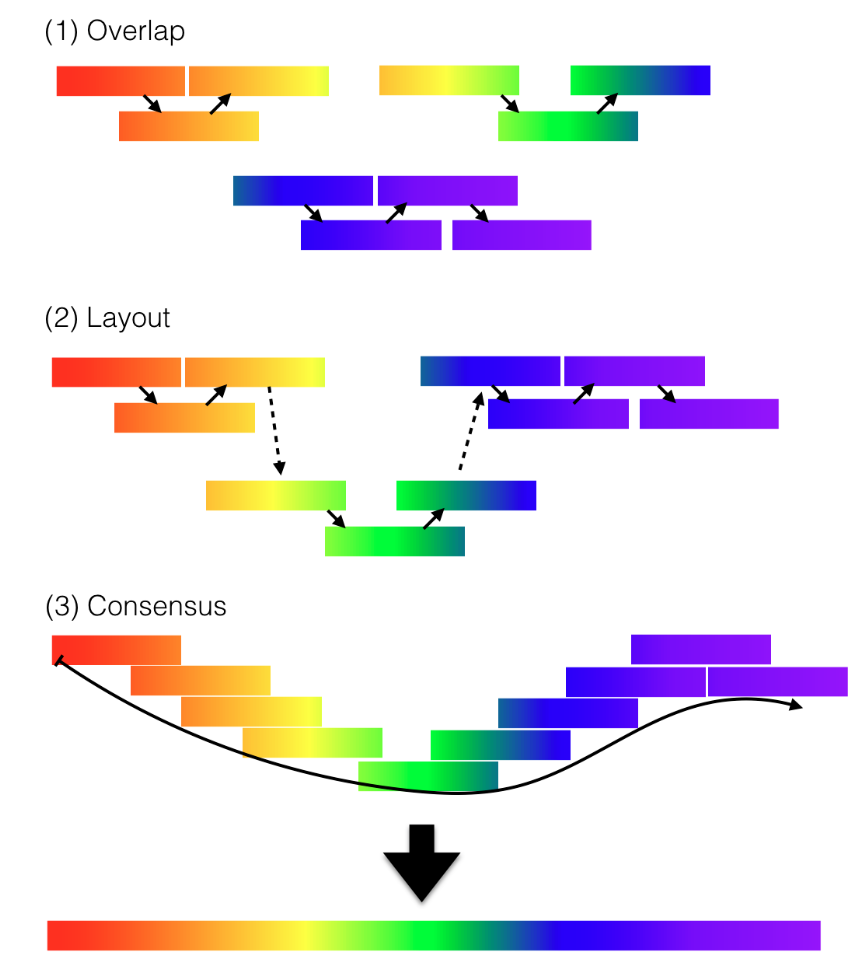
CC-BY-SA 4.0
量子アルゴリズムを用いたアセンブリ手法
アライメント(マッピング)手法については結構古くから研究されており、 Grover のアルゴリズムを塩基配列のアライメントに応用できるということが示されている (Hollenberg, 2000)。Grover のアルゴリズムは量子アルゴリズムの中では有名なため、Wikipediaをはじめいろんな記事があるのでそちらを参照していただきたい。この研究 (Hollenberg, 2000) では仮にあるゲノム(データベース)の長さが![]() であったとき、従来の計算手法では
であったとき、従来の計算手法では ![]() のオーダーであるのに対し、Grover アルゴリズムに基づく量子アルゴリズムを適用すると
のオーダーであるのに対し、Grover アルゴリズムに基づく量子アルゴリズムを適用すると ![]() まで理論上計算量を減らすことができると述べている。
まで理論上計算量を減らすことができると述べている。
2021年に Sarkar らによって提案された QiBAM というアルゴリズムも、Grover のアルゴリズムを拡張したものである (Sarkar et al., 2021)。例としてこの論文中ではヒトゲノム ![]() に対し、ショートリードシーケンサで得られた4種類の塩基(ATGC)
に対し、ショートリードシーケンサで得られた4種類の塩基(ATGC) ![]() を含む塩基配列
を含む塩基配列 ![]() のアライメントを行う場合、完全に接続された133の論理量子ビットが必要であると述べている。一応量子コンピュータのシミュレータ (OpenQL など) で検証を行っている(実機ではない)。この場合のオーダーは
のアライメントを行う場合、完全に接続された133の論理量子ビットが必要であると述べている。一応量子コンピュータのシミュレータ (OpenQL など) で検証を行っている(実機ではない)。この場合のオーダーは ![]() になると推定されている (Marchetti et al., 2022)。量子パターン認識 (quantum pattern recognition; QPR; Schützhold, 2003) を拡張したアルゴリズムも検討されている (Prousalis and Konofaos, 2019)。ただやはり現在のデータ量、シーケンス長(ロングリードへの適用)、ノイズなどを考慮すると現在実装可能かと言うとまだ時期尚早である。
になると推定されている (Marchetti et al., 2022)。量子パターン認識 (quantum pattern recognition; QPR; Schützhold, 2003) を拡張したアルゴリズムも検討されている (Prousalis and Konofaos, 2019)。ただやはり現在のデータ量、シーケンス長(ロングリードへの適用)、ノイズなどを考慮すると現在実装可能かと言うとまだ時期尚早である。
ではアセンブルにおける量子コンピュータ・量子アルゴリズムの適用はどうかというと、DBGではなくOLCアルゴリズムに基づいたアルゴリズムが提案されている。
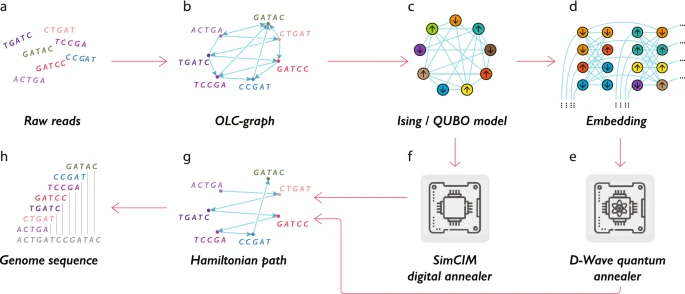
CC-BY 4.0
上の図のように、古典コンピュータ上で「量子アニーリングにインスパイアされたアルゴリズム (Tiunov et al., 2019)」に基づいてアセンブルするのと、D-Wave 社の実際の量子コンピュータ(実機)を用いたアセンブルを比較している。シーケンス長が6塩基まではD-Waveの量子コンピュータが実行速度が早いが、7塩基でシミュレータのほうが早くなり、それ以上の塩基長は実行できていない。
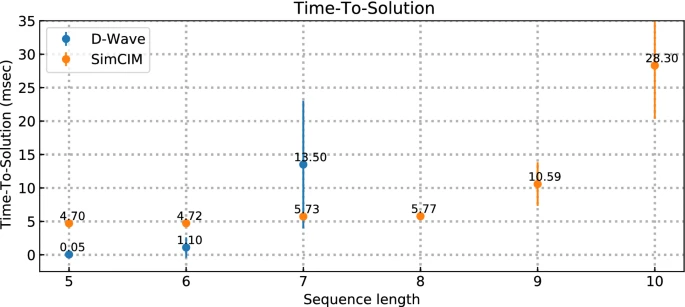
CC-BY 4.0
展望
まだ量子コンピュータの実機を用いたアルゴリズムの検証などがあまりなされていないこともあり、正確なベンチマークはこれからになるだろう。最後に紹介したD-Waveの量子コンピュータは量子アニーリング型であるため、量子ゲート型におけるアルゴリズムの開発・発展にも期待したい。昨年末にNatureに発表されたハーバード大のチーム等の論文では “These results herald the advent of early error-corrected quantum computation and chart a path towards large-scale logical processors.” と述べているように、現在主流のNISQからFTSQへのハード面での”進化”もそう遠くない未来に起こりそうな予感を示している (Bluvstein et al., 2023)。
現状、量子コンピュータを活用した生命分野、とりわけ配列解析のアルゴリズムの研究は活発とは言えない。IBMも Qiskit で実機を使って勉強できる場を用意しているものの、あまり日本人コミュニティでは記事を(まだまだ)見かけない。盛り上げていきましょう。せっかく日本国内という近所に実機があるんだからさ。
ゲノムアセンブリも量子コンピュータもまだまだ勉強中の身なので、もし誤りなどがあったらコメントで教えてくださると嬉しいです。
参考文献
- Jumper, J., Evans, R., Pritzel, A., Green, T., Figurnov, M., Ronneberger, O., … & Hassabis, D. (2021). Highly accurate protein structure prediction with AlphaFold. Nature, 596(7873), 583-589.
- Baek, M., DiMaio, F., Anishchenko, I., Dauparas, J., Ovchinnikov, S., Lee, G. R., … & Baker, D. (2021). Accurate prediction of protein structures and interactions using a three-track neural network. Science, 373(6557), 871-876.
- Marchetti, L., Nifosì, R., Martelli, P. L., Da Pozzo, E., Cappello, V., Banterle, F., … & D’Elia, M. (2022). Quantum computing algorithms: getting closer to critical problems in computational biology. Briefings in Bioinformatics, 23(6), bbac437.
- Kuhlman, B., & Bradley, P. (2019). Advances in protein structure prediction and design. Nature reviews molecular cell biology, 20(11), 681-697.
- Jagger, B. R., Kochanek, S. E., Haldar, S., Amaro, R. E., & Mulholland, A. J. (2020). Multiscale simulation approaches to modeling drug–protein binding. Current opinion in structural biology, 61, 213-221.
- Englander, S. W., & Mayne, L. (2014). The nature of protein folding pathways. Proceedings of the National Academy of Sciences, 111(45), 15873-15880.
- Perdomo-Ortiz, A., Dickson, N., Drew-Brook, M., Rose, G., & Aspuru-Guzik, A. (2012). Finding low-energy conformations of lattice protein models by quantum annealing. Scientific reports, 2(1), 1-7.
- Micheletti, C., Hauke, P., & Faccioli, P. (2021). Polymer physics by quantum computing. Physical Review Letters, 127(8), 0
- Robert, A., Barkoutsos, P. K., Woerner, S., & Tavernelli, I. (2021). Resource-efficient quantum algorithm for protein folding. npj Quantum Information, 7(1), 38.
- Canzar, S., & Salzberg, S. L. (2015). Short read mapping: an algorithmic tour. Proceedings of the IEEE, 105(3), 436-458.
- Sohn, J. I., & Nam, J. W. (2018). The present and future of de novo whole-genome assembly. Briefings in bioinformatics, 19(1), 23-40.
- Li, Z., Chen, Y., Mu, D., Yuan, J., Shi, Y., Zhang, H., … & Fan, W. (2012). Comparison of the two major classes of assembly algorithms: overlap–layout–consensus and de-bruijn-graph. Briefings in functional genomics, 11(1), 25-37.
- Hollenberg, L. C. (2000). Fast quantum search algorithms in protein sequence comparisons: Quantum bioinformatics. Physical Review E, 62(5), 7532.
- Sarkar, A., Al-Ars, Z., Almudever, C. G., & Bertels, K. L. (2021). QiBAM: approximate sub-string index search on quantum accelerators applied to DNA read alignment. Electronics, 10(19), 2433.
- Schützhold, R. (2003). Pattern recognition on a quantum computer. Physical Review A, 67(6), 062311.
- Prousalis, K., & Konofaos, N. (2019). Α quantum pattern recognition method for improving pairwise sequence alignment. Scientific reports, 9(1), 7226.
- Boev, A. S., Rakitko, A. S., Usmanov, S. R., Kobzeva, A. N., Popov, I. V., Ilinsky, V. V., … & Fedorov, A. K. (2021). Genome assembly using quantum and quantum-inspired annealing. Scientific Reports, 11(1), 13183.
- Tiunov, E. S., Ulanov, A. E., & Lvovsky, A. I. (2019). Annealing by simulating the coherent Ising machine. Optics express, 27(7), 10288-10295.
- Bluvstein, D., Evered, S. J., Geim, A. A., Li, S. H., Zhou, H., Manovitz, T., … & Lukin, M. D. (2024). Logical quantum processor based on reconfigurable atom arrays. Nature, 626(7997), 58-65.




![【Qiskit】マルチオミクス解析を量子機械学習でやる①[環境構築・基礎]](https://kimbio.info/wp-content/uploads/2024/05/2203027-100x100.jpg)