なぜ動物の性比は1:1なのか？- 個体ベースPythonシミュレーションで見る

さて，前回の話の続き．

(なぜ動物の性比は1:1なのか？-フィッシャーの原理)

前回は”概念”的な話と数式を用いた解説を行った．

それにより「両親から同じ数の遺伝子を受け継ぎ生涯性別が固定されている有性生殖をする動物」については性比がおおよそ1:1になることがわかっただろう．

今回はその現象を進化シミュレータで解明する．

Python3で作成し，実際にそのような結果になるかを追っていく．

概念は前回説明したとおりであるのでそちらを元にシミュレータを書いていく．

大まかな流れとしては，

1. ある特定の雌雄比率及びそう歪ませる遺伝子をもつ雌雄の集団を生成
2. 集団内で自由交配させ，その個体が持つ”性比遺伝子”の平均，及び特定値の分散値からなる正規分布からランダムに次世代の”性比遺伝子”の値を決定
3. それを何代にも渡って繰り返す
4. 寿命及び一様分布を設定し，それに従って個体は死亡

といった具合である．

結果

ではまずどうなるかという結果を先に述べておこう．

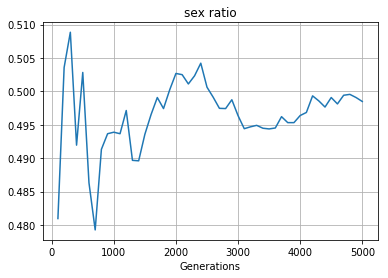
Fig.1 初期性比 雄:雌 = 0.2 : 0.8

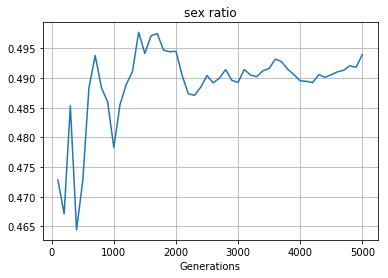
Fig.2 初期性比 雄:雌 = 0.8 : 0.2

(縦軸が雄の性比である)

このようにどちらかに非常に偏りがある集団においても最終的に代を重ねていくに連れておおよそ1:1の割合で安定していることがわかる．

今回のシミュレータでは雄も雌も交尾に関する身体的な制限は設けていないので毎秒交尾して毎秒子供を10匹産んでいるとかいうヤバイ物体であるが上手に落ち着いたと思う．

ちなみにグラフを見ると0.2始まりなのに最初のプロットがもう既に5付近にあるように見える．

立ち上がりの部分を見てみると

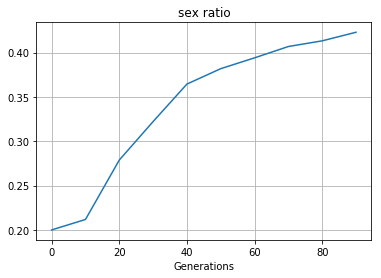
Fig.3 初期性比 雄:雌 = 0.2 : 0.8

このように非常に急速に0.5へと向かっていくのがわかる．

何も雌雄の間で制約がない状況下では性比の歪みはあまり意味を為さないのであろう．

コード解説

さてそれではコードの解説に入ろう．

全体のコードはこちら(Jupyter notebook)．

おまじない

まずはおまじない．

import numpy as np
import matplotlib.pyplot as plt
import random
from tqdm import tqdm
import statistics

……といって煙に巻くのはあまり良くないのでひとつずつ解説すると，

numpyは言わずもがな，科学計算のためのライブラリ．行列とか扱えるが，今回は専らランダムな数値を作り出すのに使う．

matplotlibはグラフ描画ライブラリ．先までの図はそれで描画した．

これらは名前が長かったりよく使うのでよく “as” をつけて略してるのをよく見る．

randomは乱数に関するライブラリ．

tqdmは長いループ処理をするときにどれだけ処理が進んでいるかをユーザー向けに可視化させるライブラリ．結構便利でforの前に入れるだけで，

こんな感じのプログレスバーを表示させることができる．

statisticsは中央値を出すのに今回使う．

個体クラス

次に個体クラスを用意する．今回はこの個体クラスしか用意しないが，何か複雑な遺伝子や要因を考えるのならば新たにゲノムクラスなどのものを加えてもいいだろう．

class Indivisual():
    def __init__(self, x):
        self.sex = np.random.choice(["m", "f"], p=[x, (1-x)])
        self.sexratio = x
        self.age = 0
        
    def death(self): # 死亡処理(0が死，1が生を意味する)
        if self.age == 10: # 10歳で確実に死ぬ
            return 0
        else:
            return np.random.choice([0, 1], p=[0.1, 0.9]) # 1/10の確率で死ぬ
        
    def spawn(self, male): # 卵を1年で10個産む
        egg = []
        for i in range(10):
            egg.append(nextGen(self.sexratio, male))
            
        return egg
    
    def aging(self): # 歳を取る
        self.age = self.age + 1

このようにメソッドを記述し，個体レベルでの処理を行わせる．

今回の主な要素としては歳(self.age)を用意し，いつまでもゾンビが集団に生き残っていることを避けるようにしてある．

またdeathメソッドで10%の確率で死にようにもしてある．これは生物によると思うので一応注意．

また今回はforの1サイクルを1年と考える．この個体は雌であればspawnメソッドから10個体子供を作る．

次世代形質の決定

次に両親の遺伝子(ここでいう遺伝子は1つの遺伝子を指すのではなく，複数の遺伝子座)から次世代の性比強度(どれだけの性比で子供を産むか)を決定する．

def nextGen(female, male): # 次世代の性比強度の決定
    ave = 0
    nextgen = -1
    
    # 両親の性比強度の平均
    ave = (female+male)/2
    # 平均ave、分散0.1の正規分布から次世代の値を決定
    while nextgen < 0 or nextgen >= 1:
        nextgen = np.random.normal(ave, 0.1)
    
    return nextgen

nextGen関数は両親の性比強度(self.sexratio)を引数とし，それらの平均をまず求める．

次にその平均及び分散0.1(これは勝手に決めた)の正規分布から次世代の子供のsex ratioをランダムに決める．

これのミソは平均からの正規分布を用いることで両親と近いながらも確率的に，平均よりも大きい/小さいsexratioを選び取ることができる．

集団内の交尾

次は交尾，交配．毎年1回交配は行われ，全集団の1/3がランダムに選ばれてその中からペアを作って交配させる．

なんで1/3かって，単純に計算量が多いから．せっかち．

def copulation(population):
    male_population = []
    female_population = []
    newgen = []
    # 計算量抑制のため，集団の1/3のみを選出，そこから交尾可能か探る
    selected_population = random.sample(population, round(len(population)/3))
    
    for i in range(len(selected_population)):
        if selected_population[i].sex == "f":
            female_population.append(selected_population[i])
        else:
            male_population.append(selected_population[i])

    if len(female_population) >= len(male_population):
        cop_i = len(male_population)
    else:
        cop_i = len(female_population)
        
    for i in range(cop_i): # 交尾させる雌雄の抽出と交配
        cop_female = female_population.pop(random.randrange(len(female_population)))
        cop_male = male_population.pop(random.randrange(len(male_population)))
        newgen.append(cop_female.spawn(cop_male.sexratio))
        
    return newgen

見てもらえればわかるが，選ばれた集団の個体を1つずつチェックして性別ごとにリストに追加，数が少ない方を交配数(カップル数)にしている(cop_i)．

最後に雌個体のメソッド，spawnを呼び出して子供をnewgenに追加して終わっている．

シミュレーション内の時間

次にこのシミュレータの「時間」を司る関数，tiktok(本来なら”tick-tock”だが)について．

def tiktok(population):
    for popu in population[:]: 
        popu.aging() # 歳を取らせてる
        if popu.death() == 0: # もし死んでいたら削除
            index = population.index(popu)
            del population[index]

    newegg = copulation(population)
    if newegg is not None:
        for i in range(len(newegg)):
            for j in range(10): 
                population.append(Indivisual(newegg[i][j]))

まず最初に各個体のagingメソッドを実行し，歳を取らせてる．その後に死亡確認を行い，死んでいる(0)場合にはその個体をpopulationから削除するということを行っている．

次にこの時間に生まれた子供の遺伝情報(sexratio)をneweggに格納し，その情報を元にインスタンスを作成．それをpopulationに加える．

人口抑制プログラム

ここまで来てお気づきの方もいるだろうが，毎年10個体，雌が産むのである．しかも生まれたら即交尾可能．populationは膨大な数に膨れ上がることが予想される．

そこで人口抑制機能を作る．

def populationControl(population, limit):
    while len(population) > int(limit):
        index = random.randrange(len(population))
        del population[index]

これによって与えられた数(limit)に達するまでランダムに集団の個体を減らし続ける．

仕上げ

さて，もうおおよその機能は書いたのであとは初期化とこれらの関数を組み合わせて実行するmain処理だけだ．

def initialize(x, firstsize): # 初期化設定
    population = []

    for i in range(firstsize):
        population.append(Indivisual(x))

    copulation(population) # 1世代目の作出
    return population

初期化は最初に与えるx値(sexratio)と最初の集団サイズから最初の集団を作り出す．これは一回だけ実行されなければならない．

次にmain処理．ここにはmatplotlibのグラフ描画も含まれる．

def main(population, iteration, limit):
    b = []
    S_x = []
    summarize = []

    for i in range(int(iteration / 10)):
        a = 0
        b.append(a+(i*10))
    
    for i in tqdm(range(iteration)):
        tiktok(population)
        populationControl(population, limit)
        
        if i in b:
            for i in range(len(population)):
                S_x.append(population[i].sexratio)
            summarize.append((statistics.median(S_x)))
                

    plt.plot(b, summarize)
    plt.title("sex ratio")
    plt.xlabel("Generations")
    plt.grid(True)

bは横軸で，どれだけの間隔でプロットするかを最初のループで決めている．

あとは書いたまま．経験則から中央値を用いているが，本当はちゃんと正規分布様になっているか確認してからのほうが良いだろう．

で，

main(initialize(0.2,50), 100, 200)

最初の初期sexratio値，初期集団サイズ，ループ回数，最大集団サイズを決めて，実行してやると，先のグラフが出力されるといった具合だ．

おわりに

今回のこれは私が卒業研究にしようと頑張っていた進化シミュレータの機能の一部を取り出してこれ用に改造したものなので若干ちぐはぐである．

しかも集団生物学を専攻していない(！)というどうしようもない学生であるので中身の保証についてはできない．

単純に「へえーおもしろいなあ」くらいに思ってもらえたら著者としては幸いである．