【Qiskit】パウリ演算子を扱う

前回に引き続き、Qiskitの勉強を続ける。今回はパウリ演算子(パウリ行列)を扱う。

パウリ行列とは

パウリ行列とは量子計算において重要な行列である。特に量子ビットの状態を操作するのに使われる。パウリ行列には以下の4つが含まれる(以下の4つをパウリ行列という)。

\[ I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \]

\[ X = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \]

\[ Y = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} \]

\[ Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \]

これらは量子ゲートとしても表記される(参考文献)。この行列同士では交換しないため、例えば\(XZ \ne ZX\)である。

from qiskit.quantum_info import SparsePauliOp

# パウリ演算子のラベルを定義
labels = ["IZ", "IX", "ZI", "XI", "ZZ", "XX"]

# SparsePauliOpオブジェクトを作成
observables = [SparsePauliOp(label) for label in labels]

# 作成された観測量を表示
for obs in observables:
    print(obs)

SparsePauliOp(['IZ'],
              coeffs=[1.+0.j])
SparsePauliOp(['IX'],
              coeffs=[1.+0.j])
SparsePauliOp(['ZI'],
              coeffs=[1.+0.j])
SparsePauliOp(['XI'],
              coeffs=[1.+0.j])
SparsePauliOp(['ZZ'],
              coeffs=[1.+0.j])
SparsePauliOp(['XX'],
              coeffs=[1.+0.j])

このようにパウリ行列のオブジェクトを作成できる。

観測可能量の計算

前回の記事に続いているので、backendは既に実行済みとしている。量子回路は以下の通りベル状態を作っている。厳密にはこの回路をパスマネージャを通じて最適な回路に変換している(isa_circuit)。

from qiskit_ibm_runtime import EstimatorV2 as Estimator

# Estimatorインスタンスの作成
estimator = Estimator(backend=backend)

# オプション
estimator.options.resilience_level = 1 # エラー修正のレベル
estimator.options.default_shots = 5000 # 量子回路の実行回数(ショット数)

# 各可観測量(オブザーバブル)を量子回路のレイアウトにマップ
mapped_observables = [
    observable.apply_layout(isa_circuit.layout) for observable in observables
]
 
# 量子回路を5つの異なる可観測量に対して実行
job = estimator.run([(isa_circuit, mapped_observables)])
 
# ジョブIDの取得
print(f">>> Job ID: {job.job_id()}")

>>> Job ID: XXXX が得られる。IBM Quantum Platform からジョブの様子は見れる。

ここで何を計算しているかというと、合成系の計算を行っている。例えば\(IZ\)、第一量子ビットに単位行列\(I\)を適用し、第二量子ビットにパウリZ行列\(Z\)を適用したものであり、以下の式で表される。

\[ I \otimes Z = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \otimes \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix} \]

["IZ", "IX", "ZI", "XI", "ZZ", "XX"] で定義しているが、この中でも\(ZZ\)と\(XX\)に着目したい。

XゲートもZゲートもブロッホ球のそれぞれX軸とZ軸周りに180度回転させるゲートである。\(XX\)も\(ZZ\)もそれぞれの量子ビットで、それぞれがX軸Z軸周りに180度回転しているはずだ(位相は異なる場合もあるが)。

ここで、観測量の期待値を計算する。ベル状態における期待値は、例えば\(\langle Z|X \rangle\)の場合、Z基底で測定すると1つ目と2つ目の量子ビットの\(Z\)成分は平均的にゼロになる。\(\langle Z|Z \rangle\)の場合では2つの量子ビットでの\(Z\)成分は相関しているため、片方を観測すればもう片方も同じ観測結果が得られるはずだ。計算結果を見てみる。

job_result = job.result()
pub_result = job.result()[0]

from matplotlib import pyplot as plt
 
values = pub_result.data.evs
 
errors = pub_result.data.stds
 
# グラフをプロット
plt.plot(observables_labels, values, '-o')
plt.xlabel('Observables')
plt.ylabel('Values')
plt.show()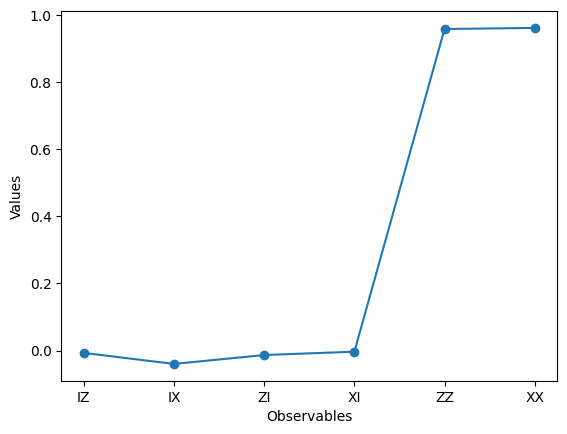

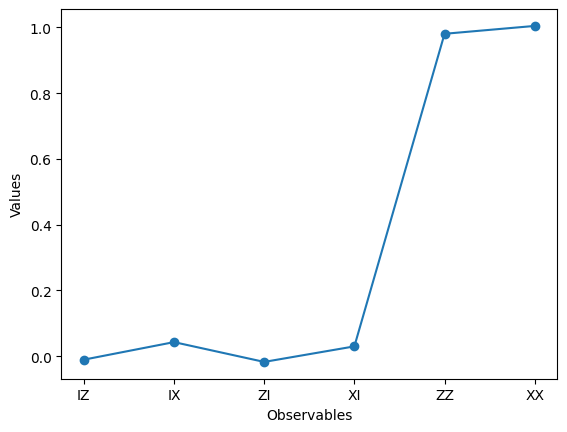
二回同じコードを実行した結果を上に示している。ここで、Valuesは各可観測量に対する期待値を示している。

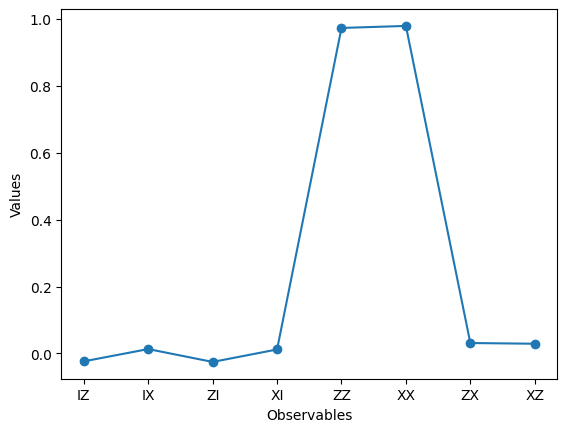
\(ZX\)と\(XZ\)についても同様に見ることができる。\(ZX\)、\(XZ\)演算子をそれぞれ作用させた場合、各量子ビットに相関は見られないことがわかる。

このグラフを見ると0であるはずのところが完全に0でなかったりする。今回5,000回試行しているが、量子コンピュータ自体のエラーがその結果に現れている。

今回量子コンピュータならではの量子ビット間での相関を実際に計算してみた。ただ前回から日が空いたように自分自身記事にできるほど量子計算の知識がないため、だいぶその計算の過程を理解するのに苦労している。しばらくは最近出た本(量子情報科学入門 第2版 Amazon)で勉強しようと思う。

量子情報科学入門 第2版 [ 石坂 智 ] 価格：4,400円（税込、送料無料) (2024/6/11時点) 楽天で購入

参考文献

• Hello World Link
• Frederic T.Chong 共著 ; 小野寺民也, 金澤直輝, 濵村一航 共訳 “量子コンピュータシステム : ノイズあり量子デバイスの研究開発” オーム社 2023.6 Amazonで買う
• 北野正雄 (2007) 「量子力学の基礎」第8章 PDF
• Yuichiro Minato 「やさしい量子ゲート操作の見直し」リンク
• 西村治道 (2023) 「量子計算量理論入門」PDF
• 東京大学素粒子物理国際研究センター (2024)【課題】量子相関を調べる リンク