今日もチュートリアルに従って進めていこうと思ったが、パスマネージャ周りで躓いたのでメモ。
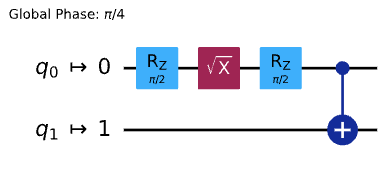
まず回路を設計する。今回は昨日の記事と同じくベル状態の回路を作る。
from qiskit import QuantumCircuit
qc = QuantumCircuit(2)
qc.h(0)
qc.cx(0, 1)
qc.draw("mpl")
測定はしていないので厳密には前回の記事とは異なるが、同じ状態を作り出している。
バックエンド
量子コンピュータを利用するといっても、全部を利用するわけではない。また、自分だけが独占して利用しているわけではなく、多くのユーザに計算リソースを適切に割り当てる必要がある。
そこで量子コンピュータのバックエンドを適切に選択してやる必要がある。下記のコードでは、least_busy で最も空いているものを探してくる。また、引数に与えているように、シミュレータではなく、動作中のコンピュータを割り当てるようにしている。
from qiskit_ibm_runtime import QiskitRuntimeService
service = QiskitRuntimeService()
backend = service.least_busy(simulator=False, operational=True)パスマネージャ
さらに、選択したバックエンド(量子コンピュータ)に対し、量子回路(ここでは上で書いたベル状態のコード)を最適化してやる必要がある。それがこのパスマネージャ (Pass manager) である。パスマネージャの役割としては、量子回路の最適化(不要なゲートの削除、ゲートの簡略化や量子回路の深さ・複雑さの軽減)とバックエンドへの最適化(ハードウェア面の最適化)、そしてエラー軽減がある。2024年6月1日現在、量子コンピュータはまだ量子誤り訂正が完全でなく、計算にエラーが含まれることがある。そのため、ノイズの影響を最小限にするためにその機器、割り当てる量子ビットの物理的な配置などを考慮して量子回路を最適化してやる必要がある。
Pythonで上の量子回路は書かれているが、それを動作しているCPUに直接上のような高級言語が与えられているわけではない。C言語とかFortranとか触っていた人だとコンパイルという手続きを踏んでいたように、CPUがわかるような形に変換してやる必要がある。
IBMの量子コンピュータも同じく、命令セットアーキテクチャ(Instruction Set Architecture; ISA) に従うように、量子回路を変換するトランスパイルを実行する必要がある。そうした諸々の面倒なことをやってくれるのがこのパスマネージャだ。以下のコードのように書かれる。
pm = generate_preset_pass_manager(backend=backend, optimization_level=1)
isa_circuit = pm.run(qc)ここではgenerate_preset_pass_manager を使用して、指定したバックエンドに最適化されたパスマネージャを生成している。optimization_level=1 はデフォルトだが、0にすると上記のような回路の最適化などをしないようにすることもできる。
実際に問い合わせるので少し時間がかかるが、返ってくる。結果を図示してみる。
isa_circuit.draw('mpl', idle_wires=False)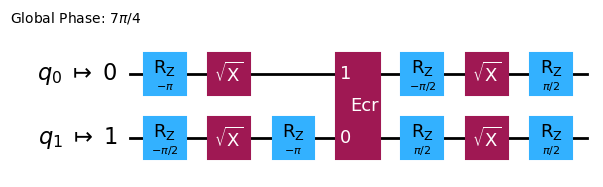
最初にPythonで書いた量子回路とはずいぶん違うように見える。そもそもチュートリアルの図ともぜんぜん違う。
例えば左上のグローバル位相 (Global phase) が違う。計算結果には影響しないようだ。おそらくボルンの規則が関わる話だと思われるが、正直わからない。厳密なところを教えて下さい。
また、\(R_z\)ゲートでZ軸周りの回転ゲートを作用させていたり、\(\sqrt{X}\)ゲート(反転ゲート)でフリップさせていたりしている。
ECRゲートも含まれている。これは簡単に言うとCNOTと同じ操作を実現するゲートである。Echoed Cross-Resonance の略であるように、エコー技術を利用して不要な量子ビット間の相互作用を消すものである。リンク先の原理の部分を見るとわかるが、事前に単一量子ビットを回転させるなどの操作をしている。ECRゲートは数式では
\[\frac{1}{2} (IX – XY)\]
で表される。
おわりに
Qiskitで簡単にHello worldができるものだと思っていたが、想像以上に複雑で、かつ難しいのでなかなか1つ1つコードを読み解くのには骨が折れる。
次回はこれらを応用して実際に量子コンピュータ上で量子もつれを見てみよう！
