あまり調べても出てこなかった上に,いちいちPython上でライブラリを使わず積分して求めるやり方とかが出てくるので覚え書きとして.
一般的に我々がよく目にする正規分布のあの釣鐘状のグラフは確率密度関数をプロットしたものである.それのプロットの仕方はそこら中に出回っているのでそちらを参照してほしい.
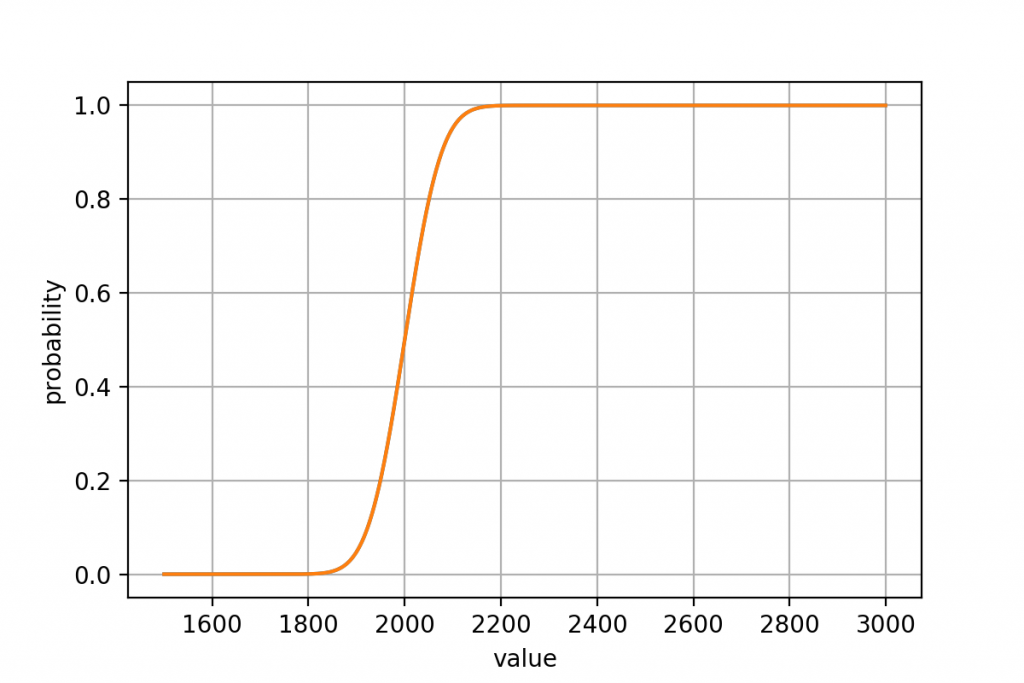
今回はこれを得たい!
累積分布関数って?
統計学的にもう一つ大事な関数として,累積分布関数(あるいは単に「分布関数」)がある.詳しい説明は省くが,要は連続確率変数Xに対して,累積分布関数![]() は
は
![]()
つまり,確率変数![]() が取る値
が取る値![]() 以下の値を取る確率,である.
以下の値を取る確率,である.
![]() が微分可能であるとき,その導関数を確率密度関数という.よく
が微分可能であるとき,その導関数を確率密度関数という.よく![]() で表されるアレである.正規分布の確率密度関数は誰もが見たことがあるだろう.
で表されるアレである.正規分布の確率密度関数は誰もが見たことがあるだろう.
![]()
また,この確率密度関数からも累積分布関数を求めることができる.
![]()
細かい数学的定義はともかくとして,今回は累積分布関数のグラフをPythonでプロットしてやりたい.より詳しい説明は統計数理の本を参照してほしい.
scipy.statsを使って累積分布関数を得る
scipyという科学計算ライブラリを今回用いる.また,Matplotlibも使う.
import numpy as np #毎度おなじみ
import matplotlib.pyplot as plt #毎度おなじみ
from scipy.stats import norm
x = np.arange(1500, 3000) # 1500~3000の要素が入ったリストを作る
y = norm.cdf(x, loc=2000, scale=60) # 平均2000,標準偏差60の正規分布の累積分布関数
plt.figure(0)
plt.grid(True)
plt.plot(x, y)
plt.xlabel("value")
plt.ylabel("probability")
plt.savefig("ruiseki.png", dpi=200)
plt.show()

scipy.statsを使えば一瞬である.最高.
気をつける部分としてはscaleには分散ではなく標準偏差,つまり分散の平方根が入る.
あまり必要となる場面は思い浮かばないが,とにかく私は卒論において一時的にこのグラフが欲しくて苦労した経験があるのでネットの海に放流しておく.



![【Qiskit】マルチオミクス解析を量子機械学習でやる①[環境構築・基礎]](https://kimbio.info/wp-content/uploads/2024/05/2203027-100x100.jpg)