今回からの記事は IBM の Qiskit で量子機械学習をマルチオミクスデータに向けてやろうというものである。昨年のカンファレンスの資料と Notebook が公開されていてダウンロードしていたのだが、論文やらなんやらで色々忙しいのを言い訳に塩漬けにしていたのをなんとか掘り起こそうという備忘録だ。量子力学100周年だしね。
【注意】2025年11月23日現在、すでにこのNotebookは公開されていません。
データのダウンロード
conda, git は既に入っているものとする。
git clone https://github.com/IBM/qml4omics.gitで資料とコードをダウンロードする。
環境構築
色々できるが、今回は conda で行う。
conda create -n qml4omics python==3.11で、環境をセットアップ。
conda activate qml4omics
cd src/
pip install -r requirements.txt
pip install notebook qiskit[visualization]必要なライブラリがこれで入る。デフォルトではNotebookが入らないので入れる。
cd ..
jupyter notebookで起動。今回の実行環境は現在の最新である
Name: qiskit
Version: 2.0.2で実行している。Apache License 2.0であることをここに明記しておく。
https://quantum.ibm.com/ にログインし、Token を取得しておく。
Hello world(実機)
早速実機を使ってみる。以前に解説記事を書いたような、簡単なところまで。やったことがある人は今はやらずに飛ばして良い。
from qiskit_ibm_runtime import QiskitRuntimeService
# アカウントトークンをこの先も使う場合、デフォルトに設定しておく
QiskitRuntimeService.save_account(channel="ibm_quantum", token="<MY_IBM_QUANTUM_TOKEN>", set_as_default=True)
# Load saved credentials
service = QiskitRuntimeService()でログイン情報を読み込み、テストジョブを実行。
from qiskit import QuantumCircuit
from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2 as Sampler
# 空のcircuitを作成
example_circuit = QuantumCircuit(2)
example_circuit.measure_all()
backend = service.least_busy(operational=True, simulator=False)
sampler = Sampler(backend)
job = sampler.run([example_circuit])
print(f"job id: {job.job_id()}")
result = job.result()
print(result)返ってくればOK。Quantum Platform からもジョブの状態を確認できる。
Quantum circuit とはなにか
(IBMのような量子ゲート方式の量子コンピュータにおける)量子プログラミングにおいて基礎となるのが Quantum circuit つまり 量子回路 である。量子回路はゲート、測定など Qubits を操作するものを含む。
Qiskit では量子回路を Python 形式で、人間にとって具体的でわかりやすい記述をすることができる。言い換えると、低レイヤのことはあまり考えなくても向こうで最適化してくれるということだ。
チュートリアルに従って回路を作ってみよう。
from qiskit import QuantumCircuit # 量子回路のモジュールのインポート
qc = QuantumCircuit(2) # 量子回路中の qbits の数を宣言
qc.qubits # 確認
# OUT
# [Qubit(QuantumRegister(2, 'q'), 0), Qubit(QuantumRegister(2, 'q'), 1)]これで2量子ビットの回路が(ローカルPC上で)仮想的に作られた。実際どうなっているか見てみよう。
qc.draw("mpl")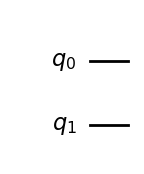
2 bits あることが確認される。
ではこれに x gate を加えてみよう。Xゲートについては以前書いた記事に詳しい。他にもYゲート、Zゲートがあり、それぞれ行列で表され、パウリ行列 と呼ばれる。
qc.x(0) # qbitの0番目にXゲートを加える
qc.data
# [CircuitInstruction(operation=Instruction(name='x', num_qubits=1, num_clbits=0, params=[]), qubits=(Qubit(QuantumRegister(2, 'q'), 0),), clbits=())]同様に回路を表示させる。
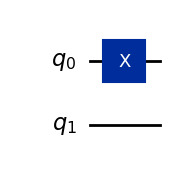
\(q_0\) にXゲートが加わった。
次に量子回路を組み合わせることをしてみよう。4 bits の量子ビットからなる回路を作ってみよう。
qc_a = QuantumCircuit(4) # 4 bits の qbit からなる量子回路
qc_a.x(0) # 0番目にXゲートを追加
qc_b = QuantumCircuit(2, name="qc_b") # 2 bits からなる量子回路。"qc_b"と名前をつける
qc_b.y(0) # 0番目にYゲート
qc_b.z(1) # 1番めにZゲート
# qc_b の 0番と1番の量子ビットを、qc_a の 1番と3番の量子ビットに対応付けて合成する
combined = qc_a.compose(qc_b, qubits=[1, 3])
combined.draw("mpl")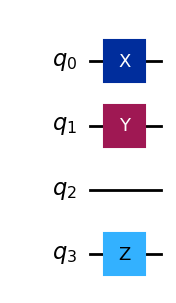
小さい量子回路を作っておいて、後で大きな回路の中に組み込んだりするときに役立つ方法である。.compose は新しい回路を返すので、もとの回路は変更されない。
量子回路の最適化
上記のパウリ演算子のようなものは最初から実装されているが、それ以外のゲートも実装したいというとき、量子コンピュータの場合ハードウェアに対して最適化を行う必要がある。これも以前の記事に詳しい。
from qiskit.circuit import Parameter
angle = Parameter("angle") # 未定義の変数(シンボリックパラメータ)
# 回路の作成(パラメトリック RXゲート)
qc = QuantumCircuit(1) # 1bit 量子回路
qc.rx(angle, 0) # qubit 0 に対して RX(angle) を適用ここで、RXゲートを追加している。RXゲートとはX軸回転ゲートであり、
\[ RX(\theta) = e^{-i\theta X/2} \]
の式で表される。今このコードの時点では angle 変数はまだ具体的な値を持たないシンボリックである。
次にトランスパイルを行う。
from qiskit.transpiler.preset_passmanagers import generate_preset_pass_manager
qc = generate_preset_pass_manager(
optimization_level=3,
basis_gates=['u', 'cx']
).run(qc)ここでは最適化レベルが3(最も高い)を指定している。他の最適化レベルとしては
0: no optimization (最適化なし)
1: light optimization (軽い最適化)
2: heavy optimization (高い最適化)
3: even heavier optimization (最も高い最適化)がある (公式ドキュメント)。
ターゲットゲートを u, cx に限定している。u は単一量子ビットのユニバーサルゲートであり、cx はCNOTゲートである。論理回路(RXゲートなど)を物理ハードウェアの実装可能なゲートで表現する記法である。これにより実行にかかる時間や誤差を減らすことができる。
Qiskitの量子回路ライブラリ
さて、今回いくつかのゲートを試したが、他にもよく使われるゲートなどがライブラリとしてQiskitに入っている。
標準的なゲートの代表格、アダマールゲート (Hadamard gate) を試してみよう。アダマールゲートは量子コンピュータならではの「重ね合わせ」の状態を作り出したりするのに使われる。アダマールゲートについては以下の記事で紹介している。
チュートリアルではさらに3制御の Toffoli ゲートを作用させる場合を考える。
from qiskit import QuantumCircuit
from qiskit.circuit.library import HGate, MCXGate
mcx_gate = MCXGate(3) # 3つの制御を持つマルチ制御Xゲート(3-control Toffoli)
hadamard_gate = HGate() # 単一のHadamardゲート
qc = QuantumCircuit(4)
qc.append(hadamard_gate, [0]) # Qubit 0 にHadamard
qc.append(mcx_gate, [0, 1, 2, 3]) # Qubits 0,1,2 → control、3 → target
qc.draw('mpl')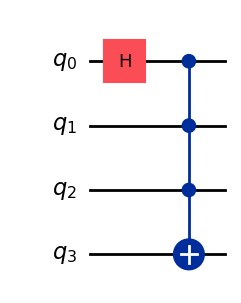
何をしているかを簡単に述べると、「アダマールゲート\(H\)を使ってQubit 0を重ね合わせ状態にし、Qubit 0, 1, 2 のすべてが 1 のときに Qubit 3 をフリップ(Xゲートを作用)」というものだ。
上の回路を言葉で表すと、「アダマールゲートのあとに3制御Toffoliゲート(MCX)を作用させる回路」である。
変分回路
次は変分回路を試してみよう。
from qiskit.circuit.library import TwoLocal
two_local = TwoLocal(3, 'rx', 'cz') # 量子ビット数3、回転ゲートrx、エンタングルメントゲートcz
two_local.draw('mpl')
ブラックボックスになってしまう! というときは
two_local.decompose().draw('mpl')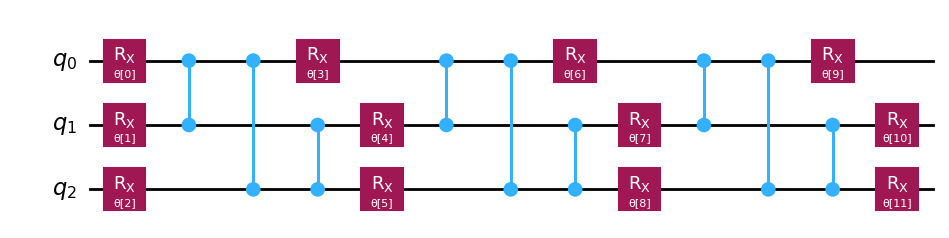
という回路図を出力できる。では何をしているのかというと、各量子ビットに対して \(rx(\theta)\) を作用させ、その後量子ビット間に cz を作用させている。回転層とエンタングルメント層を交互に配置した回路である。これをデフォルトでは3層分作っている。2層にしたいなら
from qiskit.circuit.library import TwoLocal
two_local = TwoLocal(3, 'rx', 'cz', reps=2) # reps=2
two_local.decompose().draw('mpl')
という具合で引数を与えてやる(公式ドキュメント)。
何に使うのかというと、変分量子アルゴリズム用のパラメトリック回路(ansatz; 仮定回路)に使われる。VQE(変分量子固有値ソルバ)、QAOA(量子近似最適化アルゴリズム)、QNN(量子分類器)などに使用されており、量子機械学習において重要な変分回路である。パラメータ最適化の対象となる量子回路であり、いわば量子ニューラルネットの中間層に相当する。よく使われるので TwoLocal というライブラリが用意されているということだ。
データエンコーディング回路
量子回路にデータを入れるとなると、エンコーディングが必要になる。Qiskit の方では主に3つのアプローチが用意されている。
- Amplitude encoding: 各数値を基底状態の振幅にエンコードする。実装にはコストがかかる。
- Basis encoding: 基底状態
|k>に対して整数kを符号化する。 - Angle encoding: データ内の各数値をパラメータ化された回路内の回転角度として設定する。
最適な方法はケース・バイ・ケースであるが、現在の量子コンピュータでは Angle encoding 回路を使うことが多いようだ。以下にそのうちの1つ、ZZFeatureMap の例を示す。
from qiskit.circuit.library import ZZFeatureMap
features = [0.2, 0.4, 0.8] # 入力する3次元の実数ベクトル(特徴量)
feature_map = ZZFeatureMap(feature_dimension=len(features)) # 上記に合わせた3量子ビットのエンコーディング回路
encoded = feature_map.assign_parameters(features) # パラメータを代入
encoded.draw('mpl')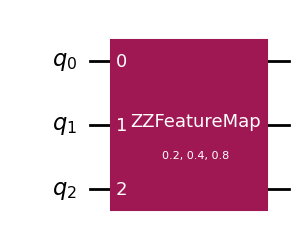
Decomposeしてやると、

こんな感じになっている。\(P(\theta) = RZ(\theta)\) である。
パウリ行列について
チュートリアルで説明しているが、こちらの記事で説明していることとだいたい同じなので割愛する。
トランスパイルについて
こちらの記事で説明している。上のようにかかれた量子回路をどうハードウェアに最適化させるかをやってくれる。現実の物理的な量子ハードウェアはすべての量子ビット間が物理的に隣り合っているわけではないので、そのあたりを実行するのがトランスパイラだ。Qiskit ではパスマネージャを作成することで量子回路のトランスパイルをすることができる。シミュレータでのやり方は後述。
パラメータなしでの基本的な量子回路の組み方
パラメータがあるような量子回路の設計に入る前に、パラメータがない量子回路を組んでみよう。Groverの量子探索アルゴリズムの一部を構築する。
from qiskit import QuantumCircuit
from qiskit.circuit.library import GroverOperator, Diagonal
from qiskit_ibm_runtime import QiskitRuntimeService
from qiskit_ibm_runtime.fake_provider import FakeSherbrooke
# Oracle の構築
oracle = Diagonal([1] * 7 + [-1]) # Diagonol は対角ゲートを構築
qc = QuantumCircuit(3) # 3量子ビット
qc.h([0, 1, 2]) # アダマールゲートを作用 → 探索空間(0-7)が同じ状態でスタート
qc = qc.compose(GroverOperator(oracle)) # Grover イテレーションをまとめたゲート
# 各量子ビットの状態を測定
qc.measure_all()
# 描画
qc.draw(output='mpl')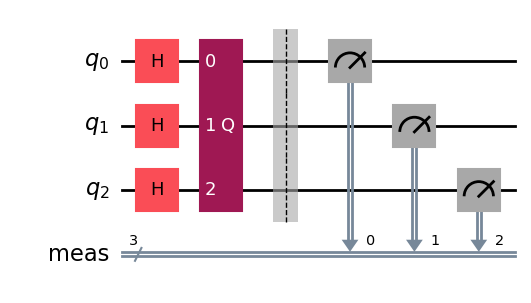
Decomposeするとこんな感じ。
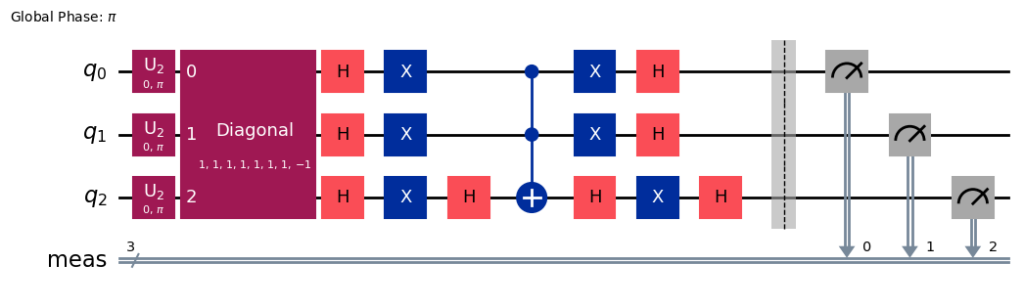
Groverの量子探索アルゴリズムは有名なアルゴリズムでもあるため、解説している記事が多い。
Oracle (オラクル) とは入力された量子状態のうち「正解」に相当する状態だけに何らかの特徴的な操作(主に位相反転)を施す関数または回路のことを指す。ここでは、
oracle = Diagonal([1, 1, 1, 1, 1, 1, 1, -1])で、状態 |111⟩ にだけ -1 の位相を与えるオラクルを作っている。
(疑似)トランスパイルのやり方
Session I での最後はトランスパイルの方法になっている。どういう情緒なのかよくわからない。
# パスマネージャの読み込み
from qiskit.transpiler.preset_passmanagers import generate_preset_pass_manager
# 量子コンピュータの設計に合わせたバックエンドを選択(ここではSherbrooke)。
backend = FakeSherbrooke()
# 最適化レベル1のパスマネージャを生成
pass_manager = generate_preset_pass_manager(optimization_level=1, backend=backend)
# 回路qcに対してパスマネージャを実行(=トランスパイルを実行)
transpiled_circ = pass_manager.run(qc)
# トランスパイル後の回路を可視化
transpiled_circ.draw(output='mpl', idle_wires=False)ちなみに、Sherbrooke (シェルブルック) はカナダの都市の名前である。他にもFakeOsaka であったり、FakeKawasaki などが存在する。去年実行したときはリージョン ibm_osaka で実行された。別に大阪にIBMの量子コンピュータ実機があるわけではない。ただのリージョン名。川崎にはあるけどね。

Open plan (無料プラン)で使えるインスタンスQPUは制限がある。2025年6月17日現在は以下の2つが使用可能だ。

すべてのQPUは
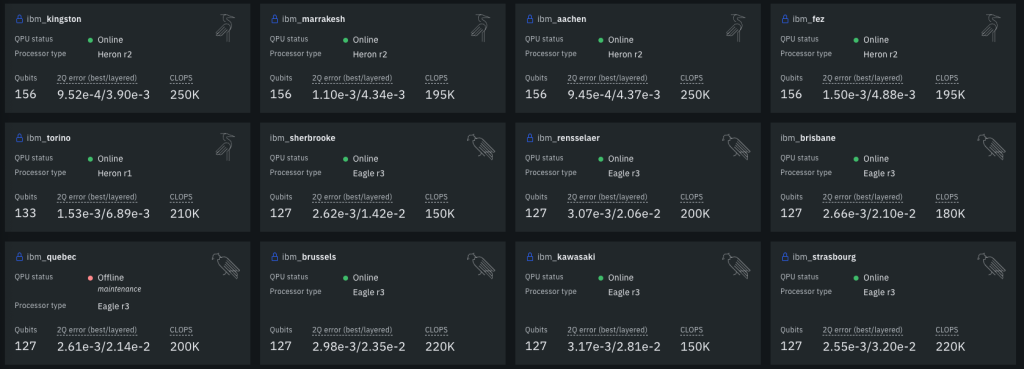
ここから見れる。Qubitsが新しい世代だとだんだん増えてる。量子ビットが今後増えるかというと先週ニュースリリースが出たように、2029年までに IBM Quantum Starling が提供され、200 論理量子ビットの実現を目指しているようだ。
IBM、新しいIBM Quantumデータセンターで世界初の大規模なフォールト・トレラント量子コンピューターの構築に着手
ここに書かれている Qubits と論理量子ビットは全く異なるもので、前者はハードウエア上に存在する量子ビットであり、ノイズが多く短時間でデコヒーレンスするのに対し、後者は(文字通り)仮想的な量子ビットでエラー耐性と長時間の動作が可能であるという違いがある。
論理量子ビットが実現されれば、またなんか量子コンピュータ関連株とか高騰しそう。
話は逸れたが、これで Session I は終了である。締まりが悪いが、次回は実際に動かしてみよう。