なぜ多くの動物の性比は1:1に保たれているのだろうか?
ヒトを例にすると、若干のゆがみはあるがおおよそ男女比は1:1である。また自然界でも多くの動物の性比は1:1であることが知られている。
一部爬虫類などでは孵化(卵がかえること)時の温度に依存して性別が決まったり、魚類でもその属するコミュニティの構成員の体の大きさによって雌雄が変化するものもあったりする。
しかし、大概はオスメスが同じくらいの比率で生まれてくる。
この記事では何故動物がこのような性比を維持しているのかを説明したフィッシャーの原理というものを解説する。また、続く記事においてPythonを用いたシミュレーションでその理論の裏付けを行う。
ゲーム理論と性比
この性比の進化の話をするにあたって避けられない理論というものがある。
フィッシャーの原理だ。
これはゲーム理論の一種で、ゲーム理論とは簡単に言えば「どのような戦略を取れば自分の利益が最大になるか」という理論である。今回のような進化の分野では「どのような戦略を取ればより多くの自分の子孫(遺伝子)を残せるか」ということを考える場合が多い.
ここにある動物の集団があることを考えて欲しい。その動物はオスとメスの比率がおよそ3:7であったとしよう。オスが少ない方だ。
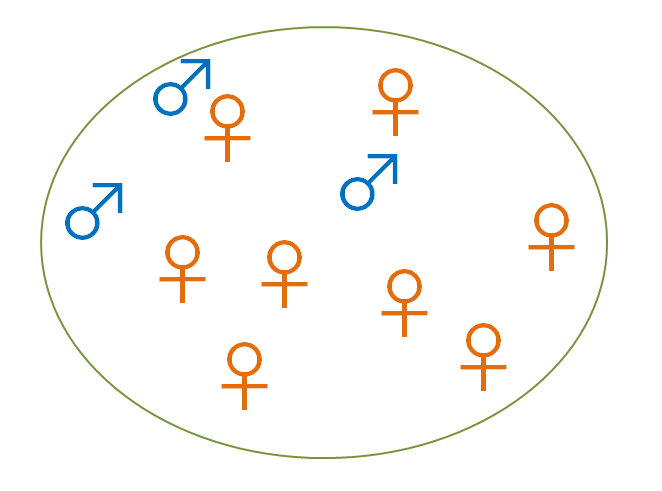
この集団のメスは一般にオスよりもメスを多く産む。
雌雄の生存率が同じという条件であれば、メスを多く産むことによってこの比率は維持されている
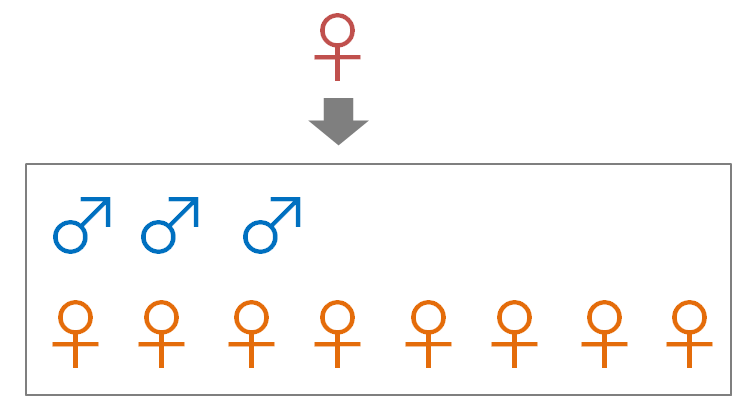
ここにある突然変異個体、「メスよりもオスを多く産む」個体が偶然生まれたとしよう。
この個体は「メスよりもオスを多く産む」という遺伝子を持った子供を産むため、この子どもたちにもその性質(遺伝子)は引き継がれる。
さて、この集団においてその子どもたちはどう振る舞うだろうか?
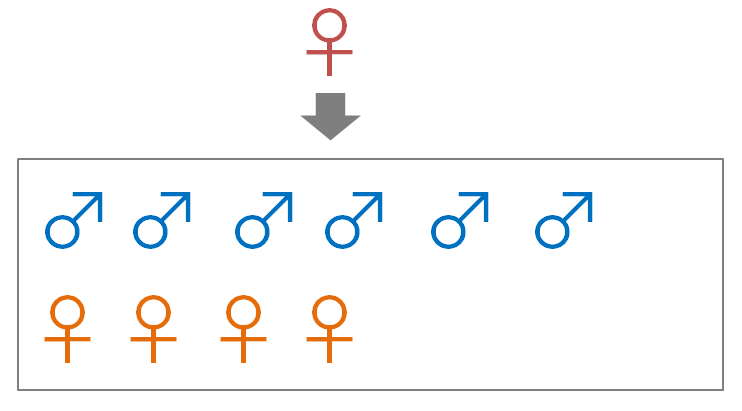
オスがもともと少ない集団であるから、その突然変異した親から生まれるオスの子供は繁殖において有利に立てる。メスのほうが多いから単純に繁殖のチャンスが多くなるのだ。
このように「オスを多く産む方が結果的に自分の子孫の数を多く増やすことができる」状態になると集団中のメスは世代を経るごとに今度はどんどんオスを多く産むような個体が増えていく。
しかしこれが集団中の殆どのメスに広がってしまうとどうなるだろうか?

このような性比で産む個体ばかりになってしまったら当然集団の性比は逆転し、オスが多い集団になってしまう。
こうなると実質的には最初と同じ状態になってしまう。
そう、そこでまた「メスを多く産む突然変異」が生じた場合、今度はその突然変異遺伝子を持つ個体が有利になり、集団に一気に広がってしまうのだ。
実際はこのように性比が逆転する前に「オスが少ないから有利」という前提が崩れ、徐々にオスを多く産むという遺伝子の変異が集団中から減っていく。
そうなることでやがてオスとメスを同じくらいの数だけ産む個体が結局有利になり、集団の性比は1:1へと収束していく。
これがフィッシャーの原理の簡単な説明である。またこの原理の考案者であるR.A. Fisherの名前からこの1:1の性比をフィッシャー性比などと呼んでいる。
数式からフィッシャーの原理を説明
ここに2n倍数体(nは自然数)の雌雄の性を終生固定された有性生殖を常にする生物を仮定する.オスとメスはその子孫に対して等しく遺伝子を受け渡すものとする.
ここに母親の繁殖成功度(自分の遺伝子を子孫にどれだけ広げられるか) ![]() を考える.また,その母親が産む次世代(子供)の数を
を考える.また,その母親が産む次世代(子供)の数を![]() ,オスの割合を
,オスの割合を![]() と置く.つまりメスの割合は(1-
と置く.つまりメスの割合は(1-![]() )となる.
)となる.
さらにその子供のうちオスの繁殖成功度を![]() ,メスの繁殖成功度を
,メスの繁殖成功度を![]() と置く.
と置く.
すると次式(1)のように母親の繁殖成功度は表すことができる.
(1) ![]()
第一項ではオスを産むことによって,母親の遺伝子がどれだけ残るかを表しており,第二項ではメスについて表してある.
さて,ここで式(1)は![]() についての一次関数であり,
についての一次関数であり,![]() について整理すると,
について整理すると,
(2) ![]()
となる.
さて,ここで母親が自由に子供の性比を決められるとする.
母親はもちろん自分の繁殖成功度 ![]() を最大値に持っていきたい.
を最大値に持っていきたい.
とすると,この(2)式において重要であるのは![]() の係数であるということがわかる.つまりこの項が最大値を取ればいい.(当然ここでは
の係数であるということがわかる.つまりこの項が最大値を取ればいい.(当然ここでは ![]() である)
である)
(i) ![]() である,つまり雄の方が繁殖成功度が高い場合
である,つまり雄の方が繁殖成功度が高い場合
![]() = 1 で最大値を取る.
= 1 で最大値を取る.
(ii) ![]() である,つまり雄も雌もどちらも同じ繁殖成功度の場合
である,つまり雄も雌もどちらも同じ繁殖成功度の場合
![]() で最大値を取る.(等号成立はするが,ここでは簡単のため考えない)
で最大値を取る.(等号成立はするが,ここでは簡単のため考えない)
(iii) ![]() である,つまり雌の方が繁殖成功度が高い場合
である,つまり雌の方が繁殖成功度が高い場合
![]() = 0 で最大値を取る.
= 0 で最大値を取る.
この![]() と
と![]() であるが,これらは集団の性比に依存している.どういうことかというと,単純に”子供”というのは”父親”と”母親”の1対のペアからのみによって生じるものであるため,雄の繁殖成功度と雌の繁殖成功度は集団全体としては同じでないといけないということである.ここでのポイントは集団全体として考えるということである.
であるが,これらは集団の性比に依存している.どういうことかというと,単純に”子供”というのは”父親”と”母親”の1対のペアからのみによって生じるものであるため,雄の繁殖成功度と雌の繁殖成功度は集団全体としては同じでないといけないということである.ここでのポイントは集団全体として考えるということである.
雌の繁殖成功度はその個体の産んだ子供の数で決まるが,雄の繁殖成功度は受精させた卵の数によって決まる.
雄が複数の雌の卵を受精させようとも,次世代の子供はすべて親の雄が誰であろうか関係なく”雄と雌から生じた”という前提から成り立っているので,”集団全体としては”雄の繁殖成功度も雌の繁殖成功度も同じになる,というかならないといけないということである.(ちょっとややこしいが)
さて,ここで集団中の母親が![]() 匹いることを仮定する.それらの雌全員が
匹いることを仮定する.それらの雌全員が![]() の性比で子供を産むとすると,先の集団全体の繁殖成功度は雌雄で等しいという前提から次の式が求まる.
の性比で子供を産むとすると,先の集団全体の繁殖成功度は雌雄で等しいという前提から次の式が求まる.
(3) ![]()
ここで,雄のみ産むという ![]() = 1 の場合,式(3)の右辺が0になり,等号不成立となり不適.
= 1 の場合,式(3)の右辺が0になり,等号不成立となり不適.
同じく雌のみ産むという ![]() = 0 の場合も式(3)の左辺が0となり不適.
= 0 の場合も式(3)の左辺が0となり不適.
つまり,雌雄どちらかの繁殖成功度が大きい場合はどちらも式(3)が成り立たない.
残るはどちらも繁殖成功度が等しい(![]() )場合,つまり
)場合,つまり ![]() のときであるが,これは
のときであるが,これは ![]() = 0.5 の時に式(3)が成立する.
= 0.5 の時に式(3)が成立する.
よって,集団中の性比は1:1になる,という結論が導き出される.
数式から性比が1:1になるであろうことは導き出すことはできたが,ピンとこない人のために個体ベースモデルによるシミュレーションを作成した.次のシミュレーションの記事に続く.
なぜ動物の性比は1:1なのか?- Pythonシミュレーションで見る
参考文献リスト
- 巌佐 庸・舘田 英典(2015) 「集団生物学」p108~p110





![【Qiskit】マルチオミクス解析を量子機械学習でやる①[環境構築・基礎]](https://kimbio.info/wp-content/uploads/2024/05/2203027-100x100.jpg)


ピンバック:なぜ動物の性比は1:1なのか?- Pythonシミュレーションで見る – Kim Biology and Informatics