【Python】GPyでガウス過程回帰と予測をやってみる

はじめに

ガウス過程回帰とは，線形回帰ではフィッティングできないようなものであってもより有効な非線形回帰モデルの1つである．

説明変数xを入力として，目的変数yを導き出す．

詳しい説明は以下の文献を参照して欲しい．(ぶっちゃけ私は詳しいガウス過程回帰の仕組みとかよくわかっていない．「こういうのがあるから使ってみるといいよ～」って言われたまま使ってるだけ……)

赤穂昭太郎. (2018). ガウス過程回帰の基礎. システム/制御/情報, 62(10), 390-395.

今回はPythonのライブラリのひとつである”GPy”を用いてこのガウス過程回帰を行う．

ただし用途がやや特殊でOpenPoseの動画データを解析するというものであるため，あまり実データ範囲外の予測は主眼にはない．

OpenPose for Unity で人の動きを二次元に落とし込む
　Ubuntu18.10にopenposeをインストール(環境構築)

今回はこれを得たい！

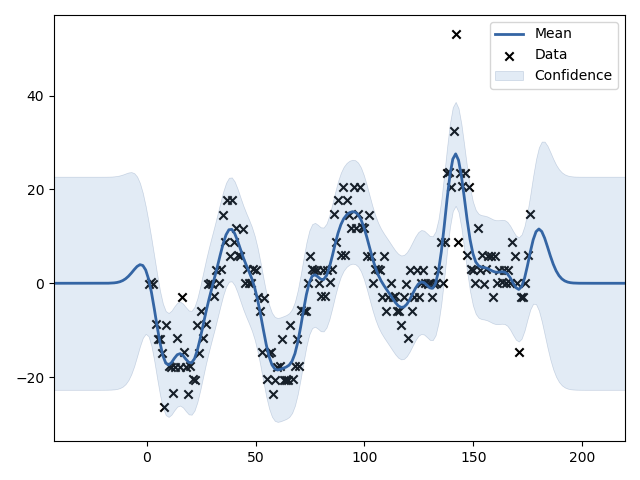
こういった入力データに対する非線形な回帰曲線を得たい．

さらに今回はこの得られた回帰曲線から説明変数を入力し，目的変数を取り出すところ(つまり予測)までを行う．

GPyのインストール

Anacondaもしくはminicondaの使用を推奨する．

このGPyは前提としてscipyが必要なのでまずは，

conda update scipy

でscipyを最新版にしておく．GPyでは 0.16 以上のscipyを推奨している．

次にGPyのインストール．

pip install gpy

以上でGPyのインストールは完了だ．

回帰曲線をプロットする

今回はGPy以外にnumpy, pandas, matplotlib を使う．Anaconda等を入れている場合はbaseに入っていたりするので特別導入はしなくていいが，もしネイティブのPythonを叩いたりしている場合はインストールしておくように．

プロットの部分は以下の記事を参考にしている．

GPy（Pythonのガウス過程用ライブラリ）の使い方

また，今回使うデータは以下のデータ．ある動画を解析したもので(言ってしまえばOpenPoseで吐き出されるデータ)，1フレームごとのとある関節の座標を示している．これの1フレームごとの動きの差分を取り出し，それをy値とし，フレーム数をx値としたい．

まずはじめにimport

import GPy
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

d = pd.read_csv("./testdata.csv")
kernel = GPy.kern.RBF(1)
model = GPy.models.GPRegression(d.index.values[1::, None], d.data.diff()[1::, None], kernel=kernel)
model.optimize()
model.plot()
plt.savefig('hoge.png')

その後，CSVを読み込み，カーネルを定義する．今回はRBFカーネルを用いた．入力次元は1次元．

次にmodelインスタンスを作成する．Gaussian Process Regression(GPRegression)を用いる．引数は X, Y, kernel=None, Y_metadata=None, normalizer=None, noise_var=1., mean_function=None 　なので必ずXとYは入れてやらないといけない．

今回はXはフレーム(進んだ時間)にしたいので，読み込んだCSVのindexを取ってきている．

Yは各フレームの差分を取ってきたいのでdiffメソッドを呼び出す．

軽く注意しておくこととしては差分を取っているので0番目の要素が空になる．そのため1から最後までをスライスしてやってる．

kernelは最初に定義したRBFカーネルを使う．

そしてその生成したインスタンスをoptimizeメソッドで最適化してからプロットしてやる．Jupyter notebookとか使ってるならおそらく表示されるだろうが，今回は保存しておきたかったのでsavefigしてある．

とりあえずこれでこの図がプロットできたはずだ．

データの予測を行う

次にこの曲線の関数を得たかった……のだが，どうやらそういう出力機能は実装されていないらしいので，生成したmodelインスタンスをそのまま用いて予測を行う．

日本語で紹介しているところがなくてオゲーってなりながら公式ドキュメントを読んでいたら書いてあったのでメモ程度に．

Coregionalization with Gaussian Processes

予測したい範囲(X)を設定しmodel.predictメソッドで予測を行う．

def prediction(model):
    # prediction
    newX = np.arange(0,20)[:,None]
    newX = np.hstack([newX,np.ones_like(newX)])
    noise_dict = {'output_index':newX[:,1:].astype(int)}

    print(model.predict(newX,Y_metadata=noise_dict))

出力は，

(array([[  2.17007152],
       [  0.51169308],
       [ -1.67059691],
       [ -4.27015813],
       [ -7.11180983],
       [ -9.97031183],
       [-12.60120318],
       [-14.77946093],
       [-16.33894159],
       [-17.20431356],
       [-17.40769538],
       [-17.08466669],
       [-16.44845925],
       [-15.74620374],
       [-15.20591947],
       [-14.9861156 ],
       [-15.14026284],
       [-15.60547768],
       [-16.2189848 ],
       [-16.75871401]]), array([[43.81702329],
       [37.82596605],
       [34.34901654],
       [32.72801827],
       [32.18903604],
       [32.10170809],
       [32.10148058],
       [32.06424222],
       [31.99960328],
       [31.94693567],
       [31.92275085],
       [31.91825546],
       [31.91816656],
       [31.91470414],
       [31.9087051 ],
       [31.90376527],
       [31.90153392],
       [31.90116658],
       [31.90114016],
       [31.90071735]]))

のように出てくる．

これの1つめのarrayが予測したい範囲XにおけるY値だ．

おわりに

あまりガウス過程回帰をよく理解していないが，とりあえずGPyで回帰曲線を得たくて，その回帰曲線を用いて実データ範囲内の予測を行いたかった．

本当はカーネルがいろいろあったりとかするのだが，別のブログ等を参照していただきたい．ただこのGPyはあまり日本語で紹介しているサイトがないので苦労する気がする……．

またGPyで本当はオンライン学習のように新たに追加されたデータに対して回帰曲線を補正していく，みたいなことをやりたかったのだが，どうにも今の段階ではその機能は追加されていない模様．

本当に何もわかっていない素人丸出しの記事になってしまった．もし誤解をしているような箇所や補足があったらこっそりコメントで教えていただけると大変助かります．